A thin lens has focal length / and its aperture diameter d. It forms an image of intensity/. Now the central part of the aperture upto diameter d2 is blocked by an opaque paper. Find out the change of focal length and intensity.
Original intensity of image = I
Amount of blocked area
=π(d2)2πd2=πd24πd2=14
Hence, new intensity, I.=I−I4=3I4
Similar Questions
A thin lens focal length f and its aperture has diameter d. It forms an image of intensity I. Now the central part of the aperture up to diameterd2 is blocked by an opaque paper. The focal length and image intensity will change to
View SolutionA lens having focal length f and aperture of diameter d forms an image of intensity I. Aperture of diameter d/2 in central region of lens is covered by a black paper. Focal length of lens and intensity of image now will be respectively
View Solution
Knowledge Check
A thin lens focal length f1 and its aperture has diameter d. It forms an image of intensity I. Now the central part of the aperture up to diameterd2 is blocked by an opaque paper. The focal length and image intensity will change to
Af2 and I2Bf and I4C3f4 and I2Df and 3I4A thin convex lens of focal length f, has its aperture of diameter d. It forms a real iomage of intensity I. The central part of the aperture is blocked by an opaque paper of diameter d2. What is the focal length of the lens and the intensity of image formed by the lens ?
Af2,I2Bf,3I4C3f4,12Df,I4A lens having focal length f and aperture of diameter d forms an image of intensity I. Aperture of diameter d2 is central region of lens is covered by a black paper. Focal length of lens and intensity of image now will be respectively.
Afand3I4Bf2andI2CfandI4D2f
Calculate the focal length of a lens, if its power is - 2.5 D
View SolutionA lens having focal length f and aperture of diameter d forms an image of intensity I. Aperture of diameter d/2 in central region of lens is covered by a black paper. Focal length of lens and intensity of image now will be respectively
View SolutionA lens haivng focal length and aperture of diameter d forms an image of intensity I. Aperture of diameter d2 in central region of lens is covered by a black paper. Focal length of lens and intensity of image now will be respectively.
View SolutionA lens haivng focal length and aperture of diameter d forms an image of intensity I. Aperture of diameter d2 in central region of lens is covered by a black paper. Focal length of lens and intensity of image now will be respectively.
View SolutionShown an object and its image formed by a thin lens. Then the nature and focal length of lens is
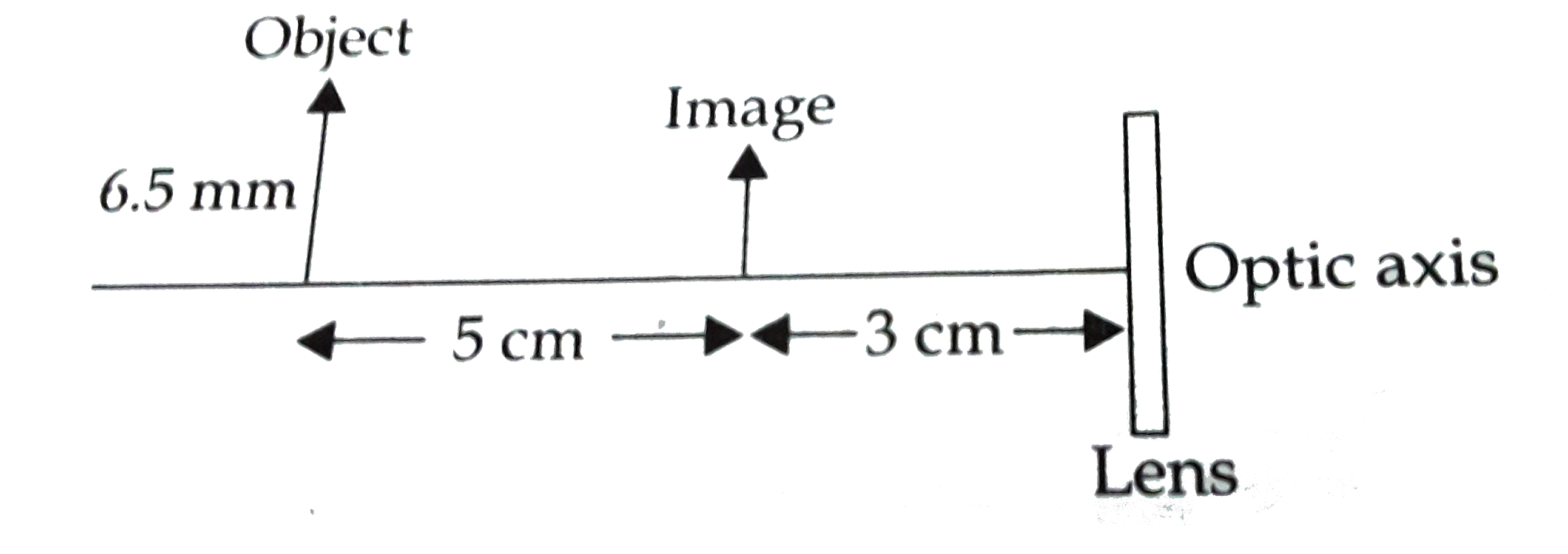
View Solution
