Derive spherical mirror formula $\frac{1}{v} + \frac{1}{u} = \frac{1}{f^{'}}$ where all the symbols have their usual meaning.

Text Solution

Verified by Experts

(i)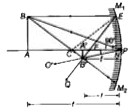
In about figure, triangles $A^{.} B^{.} F^{.}$ and ENF are similar such that
$\frac{A^{.} B^{.}}{N E} = \frac{A^{.} F}{N F}$
Since, the aperture of concave mirror is small, therefrom $N F \approx and N E = A B$ ,such that
$\frac{A^{.} B^{.}}{A B} = \frac{A^{.} F}{P F}$
As, $A^{.} F = P A^{.} - P F^{.}$
$∴ \frac{A^{.} B^{.}}{A B} = \frac{P A^{.} - P F}{P F}$
Also, $\frac{A^{.} B^{.}}{A B} = \frac{P A^{.}}{P A}$
$(∴ triangles ABP and A^{.} B^{.} P are similar)$
From Eqs. (i) and (ii), we get
$\frac{P A^{.} - P F}{P F} = \frac{P A^{.}}{P A}$
Using sign convention, $P A = - u, P A^{.} = - V$ and $P F = - f$ Subsitituting the values in Eq. (iii), we get
$\frac{v - (- f)}{- f} = \frac{- v}{- u} \Rightarrow \frac{v - f}{f} = \frac{v}{u} \Rightarrow \frac{v}{f} - 1 = \frac{v}{u}$
Dividing both sides by v, we get
$\frac{1}{f} = \frac{1}{v} + \frac{1}{u}$
That is the mirror formula for real image formed by spherical mirror.

Updated on:21/07/2023

The mirror formula is given by
$\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$
where the symbols have their usual meanings. Then the lens formula is given by
A $\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$
B $\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$
C $\frac{1}{v} + \frac{1}{u} = - \frac{1}{f}$
Dnone of these
What is the dimensional formula of $\frac{1}{μ_{0} ε_{0}}$ where the symbols have their usual meanings?
A $[M^{0} L^{2} T^{2}]$
B $[M^{0} L^{2} T^{- 2}]$
C $[M^{0} L^{- 1} T^{2}]$
D $[M^{0} L^{1} T^{- 1}]$