Show what universal gas constant represents work done per degree per mole ?
To show what the universal gas constant (R) represents in terms of work done per degree per mole, we can follow these steps:
Step 1: Understand the Ideal Gas Equation
The ideal gas equation is given by:
PV=nRT
Where:
- P = Pressure
- V = Volume
- n = Number of moles
- R = Universal gas constant
- T = Temperature in Kelvin
Step 2: Rearranging the Ideal Gas Equation
We can rearrange the equation to express R:
R=PVnT
Step 3: Analyzing the Units of R
The value of the universal gas constant R is approximately 8.314J K−1mol−1. Here, we can break down the units:
- P (Pressure) is in Pascals (Pa)
- V (Volume) is in cubic meters (m³)
- n (Number of moles) is in moles (mol)
- T (Temperature) is in Kelvin (K)
Step 4: Work Done Representation
In thermodynamics, the work done W is represented as:
W=PV
Thus, substituting W into the equation for R:
R=WnT
Step 5: Interpreting R as Work Done per Degree per Mole
From the equation R=WnT, we can interpret it as:
- W (Work done) in joules (J)
- n (Number of moles) in moles (mol)
- T (Temperature) in Kelvin (K)
This means that R represents the work done per mole per degree of temperature:
R=Work done (J)Number of moles (mol)×Temperature (K)
Conclusion
Thus, the universal gas constant R can be understood as the amount of work done (in joules) per mole of gas for each degree of temperature change.
---
The ideal gas equation is given by:
PV=nRT
Where:
- P = Pressure
- V = Volume
- n = Number of moles
- R = Universal gas constant
- T = Temperature in Kelvin
We can rearrange the equation to express R:
R=PVnT
The value of the universal gas constant R is approximately 8.314J K−1mol−1. Here, we can break down the units:
- P (Pressure) is in Pascals (Pa)
- V (Volume) is in cubic meters (m³)
- n (Number of moles) is in moles (mol)
- T (Temperature) is in Kelvin (K)
In thermodynamics, the work done W is represented as:
W=PV
Thus, substituting W into the equation for R:
R=WnT
From the equation R=WnT, we can interpret it as:
- W (Work done) in joules (J)
- n (Number of moles) in moles (mol)
- T (Temperature) in Kelvin (K)
R=Work done (J)Number of moles (mol)×Temperature (K)
Thus, the universal gas constant R can be understood as the amount of work done (in joules) per mole of gas for each degree of temperature change.
Similar Questions
Knowledge Check
- Question 1 - Select One
If R= universal gas constant, the amount of heat needed to raise the temperature the temperature of 2mol of an ideal monatomic gas from 273K to 373K when no work is done is
Aa. 100RBb. 150RCc. 300RDd. 500R
What does the universal gas constant signify?
View SolutionOne mole of an ideal monoatomic has is taken through cyclic process ABC as shown in the graph with pressure and temperature as coordinate axes. Process AB is defined as PT = constant. Take universal gas constant to be R. Then:
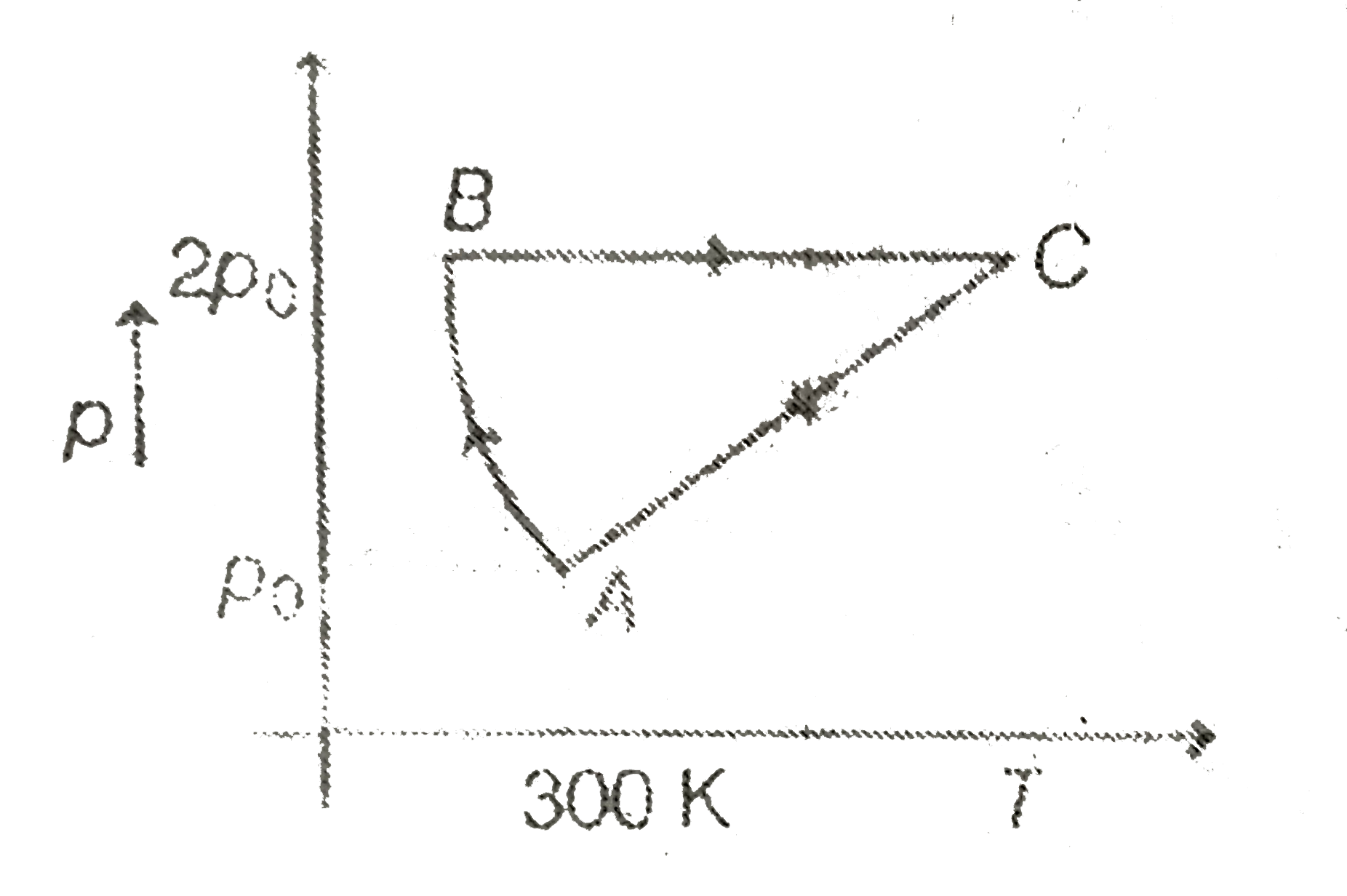
work done on gas in the process AB isView SolutionWork done per unit time
View SolutionFor one mole of a diatomic gas, the ratio of heat transfer at constant pressure to work done by the gas is
View SolutionWhat is universal gas constant ? Derive its value in different scales of measurements.
View SolutionThe equation of state of a gas is given as P(V-b)=nRT, where b is constant ,n is the number of moles and R is the universal gas constant .when 2 moles of this gas undergo reversible isothermal expansion from volume V to 2V ,what is work done by the gas ?
View SolutionThe vander waal's equation for a gas is (p+aV2)(V−b)=nRT where p, V, R, T and n represent the Pressure, Volume, universal gas constant, absolute temperature and number of moles of a gas respectively, where a and b are constants. The ratioba will have the following dimensional formula
View Solution

