Calculate the angle at which first order reflection will occur in an X-ray spectrometer when X-rays of wavelength 1.54Å are diffracted by the atoms of a crystal given that interplanar distance is 0.04Å.
To calculate the angle at which first order reflection will occur in an X-ray spectrometer, we will use Bragg's Law, which is given by the equation:
nλ=2dsinθ
Where:
- n = order of reflection (for first order, n=1)
- λ = wavelength of the X-rays
- d = interplanar distance
- θ = angle of diffraction
1. Identify the given values:
- Wavelength of X-rays, λ=1.54Å
- Interplanar distance, d=0.04Å
- Order of reflection, n=1
2. Substitute the values into Bragg's Law:
nλ=2dsinθ
Substituting the known values:
1×1.54=2×0.04sinθ
3. Simplify the equation:
1.54=0.08sinθ
4. Solve for sinθ:
sinθ=1.540.08
sinθ=19.25
5. Since sinθ cannot be greater than 1, we should check the calculations again.
- Re-evaluate the calculation:
sinθ=1.542×0.04=1.540.08=19.25
This indicates that the values provided may not yield a valid angle for first order reflection.
Conclusion:
Given the values, the calculation indicates that the angle cannot be determined because sinθ exceeds 1. This suggests that the conditions for first order reflection are not met with the provided interplanar distance and wavelength.
- n = order of reflection (for first order, n=1)
- λ = wavelength of the X-rays
- d = interplanar distance
- θ = angle of diffraction
- Wavelength of X-rays, λ=1.54Å
- Interplanar distance, d=0.04Å
- Order of reflection, n=1
nλ=2dsinθ
Substituting the known values:
1×1.54=2×0.04sinθ
1.54=0.08sinθ
sinθ=1.540.08
sinθ=19.25
- Re-evaluate the calculation:
sinθ=1.542×0.04=1.540.08=19.25
This indicates that the values provided may not yield a valid angle for first order reflection.
Given the values, the calculation indicates that the angle cannot be determined because sinθ exceeds 1. This suggests that the conditions for first order reflection are not met with the provided interplanar distance and wavelength.
Similar Questions
An X-ray has a wavelength of 0.010 Å. Its momentum is
View SolutionX-rays of λ=1Å have frequency
View SolutionFor Bragg's diffraction by a crystal to occur, then the X-ray of wavelength λ and interatomic distance d must be
View SolutionDtermine the accelerating potential necessary to given an electron a de Broglie wavelength of 17Å, which is the size of the interatomic spacing of atoms in a crystal
View SolutionOn operating an X-ray tube at 1 kV. X-rays of minimum wavelength 6.22Å are producd. I fht tube is operated at 10kV, then the minimum wavelength of X-rays prodcued will be
View SolutionA grating has 5.7×103 lines per cm. If X-rays of wavelength 546 nm are incident on the grating, find the angle of reflection for the first order diffraction maximum.
View SolutionAn X-ray tube operated at 40kV emits a continous X-ray spectrum with a short wavelength limit λmin=0.310Å. Calculate Plank's constant.
View SolutionA material whose K -absorption edge is 0.2Å is irradiated by X-ray of wavelength 0.15Å , find the maximum energy of the photoelectrons that are emitted from the K shell.
View SolutionIn a diffraction pattern due to single slit of width 'a', the first minimum is observed at an angle 30∘ when light of wavelength 5000Å is inclined on the slit. The first secondary maximum is observed at an angle of:
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
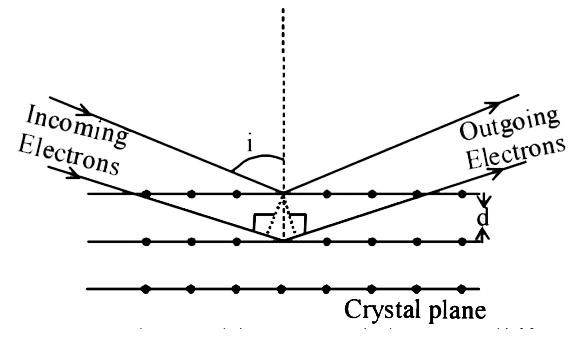
If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength λdB of electrons can be calculated by the relationship (n is an intenger)
View Solution
