A compount AB has a rock type structure with A:B=1:1. The formula weight of AB is 6.023Yamu and the closed A−B distance is Y1/3nm.
(i) Find the density of lattice.
(ii) If the density of lattice is found to be 20kgm−3, then predict the type of defect.
Calculations of the density of unit cell.
Density (ρ)=Z×MN0×(a)3
For Rock salt structure (Z) = 4 , M = 6.022 Y amu = 6.022 g mol−1
N0=6.022×1023mol−1,a=2Y1/3nm=(2×Y1/3×10−9m)
∴ Density(ρ)=4×(6.022Y g mol−1)(6.022×1023mol−1)×(2×Y1/3×10−9mol)3
=5×103g mol−1=5 kg mol−1
(b) Type of the point defect.
The measured density of unit cell = 20 kg m−3
Since the measured density of unit cell is very high as compared to calculate density, the crystal suffers from metal excess defect.
Similar Questions
A compound AB has a rock salt type structure with A:B=1:1 . The formula weight of AB is 6.023 y amu and the closest A-B distance is y1/3 nm. Calculate the density of lattice (in kg/m3)
View SolutionA binary salt AB (formula weight = 6.023 Y amu, where Y is an arbitray number) has rock salt structure with 1:1 ratio of A to B. The shortes A - B distance in the unit cell is Y1/3nm.
(a) Calculate the density of the salt in kgm−3
(ii) Given that the measured denstiy of the salt is 20kgm−3, specify the type of point defect present in the crystal
View SolutionThe crystal AB (rock salt structure) has molecular weight 6.023 y u, where y is an arbitrary number in u. If the minimum distance between cation and anion is y1/2 nm and the observed density is 20kg/m3, find the (i) density in kg/m3 and (ii) type of defect.
View SolutionThe crystal AB(rock salt structure) has molecular weight 6.023Yu, where Y is an arbitrary number in u. If the minimum distance between cation and anion is Y13nm. Find the density in kgm−3.
View SolutionA is a point on the y-axis whose ordinate is 5 and B = (-3,1) .Find AB.
View SolutionAB crystallizes in a rock salt structure. The nearest distance between A and B is Y1/3 nm, where Y is a constant. The molecular mass of AB is 6.023 Y g/mol−1 .Determine the density in kgm−3.
View SolutionA line AB meets X-axis at A and Y-axis at B. P(4, -1) divides AB in the ratio 1:2.
(i) Find the coordinates of A and B.
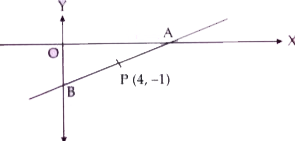
View SolutionIf the lattice parameter of Si=5.43Å and the mass of Si atom is 28.08×1.66×10−27kg, the density of silicon in kgm−3 is (Given: Silicon has diamondcubic structure)
View SolutionA line AB meets the x-axis at A and the y-axis at B. P(4,-1) divides AB in the ratio 1:2
(i) Write down the co-ordinates of A and B.
(ii)find the equation of the line through p and perpendicular to AB

View SolutionA line AB meets X-axis at A and Y-axis at B. P(4, -1) divides AB in the ratio 1:2.
(ii) Find the equation of the line through P and perpendicular to AB
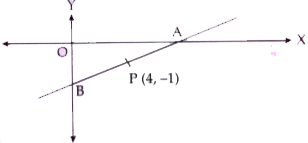
View Solution
