In which of the following arrangements, Octahedral voids are formed ?
hcp
bcc
simple cubic
fcc.
The correct Answer is:A, D
To determine in which arrangements octahedral voids are formed, we need to analyze the structures mentioned in the options: Simple Cubic (SCP), Body-Centered Cubic (BCC), and Face-Centered Cubic (FCC).
1. Understanding Octahedral Voids:
- Octahedral voids are formed when atoms are arranged in such a way that there are empty spaces that can accommodate another atom. These voids are typically located at specific positions in the unit cell.
2. Analyzing Simple Cubic (SCP):
- In a Simple Cubic structure, atoms are located at the corners of the cube.
- The only octahedral void present is at the body center of the cube.
- Therefore, octahedral voids are formed in the Simple Cubic structure.
3. Analyzing Body-Centered Cubic (BCC):
- In a Body-Centered Cubic structure, there are atoms at each corner and one atom at the center of the cube.
- The body center is occupied by an atom, and there are no additional octahedral voids present.
- Thus, octahedral voids are not formed in the BCC structure.
4. Analyzing Face-Centered Cubic (FCC):
- In a Face-Centered Cubic structure, atoms are located at each corner and at the centers of each face of the cube.
- Octahedral voids are present at the body center and at the edge centers of the cube.
- Therefore, octahedral voids are formed in the FCC structure.
5. Conclusion:
- Based on the analysis:
- Octahedral voids are formed in Simple Cubic (SCP) and Face-Centered Cubic (FCC) arrangements.
- They are not formed in Body-Centered Cubic (BCC).
Final Answer:
The arrangements in which octahedral voids are formed are:
- Option A: Simple Cubic (SCP)
- Option D: Face-Centered Cubic (FCC)
- Octahedral voids are formed when atoms are arranged in such a way that there are empty spaces that can accommodate another atom. These voids are typically located at specific positions in the unit cell.
- In a Simple Cubic structure, atoms are located at the corners of the cube.
- The only octahedral void present is at the body center of the cube.
- Therefore, octahedral voids are formed in the Simple Cubic structure.
- In a Body-Centered Cubic structure, there are atoms at each corner and one atom at the center of the cube.
- The body center is occupied by an atom, and there are no additional octahedral voids present.
- Thus, octahedral voids are not formed in the BCC structure.
- In a Face-Centered Cubic structure, atoms are located at each corner and at the centers of each face of the cube.
- Octahedral voids are present at the body center and at the edge centers of the cube.
- Therefore, octahedral voids are formed in the FCC structure.
- Based on the analysis:
- Octahedral voids are formed in Simple Cubic (SCP) and Face-Centered Cubic (FCC) arrangements.
- They are not formed in Body-Centered Cubic (BCC).
The arrangements in which octahedral voids are formed are:
- Option A: Simple Cubic (SCP)
- Option D: Face-Centered Cubic (FCC)
Similar Questions
Knowledge Check
Which of the following statements is not about the voids ?
AOctahedral void is formed at the centre of six spheres which lies at the apices of a regular octahedronBThere is one octahedral site for each sphereCThere are two tetrahedral sites for each sphereDOctahedral voids are formed when the triangular voids in second layer exactly overlap with similar voids in the first layer .
What is the coordination number of octahedral voids?
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the figure given below, the site marked as S is a
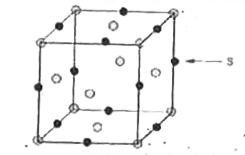
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In Schottky defect
View SolutionWhich of the following is not true about the voids formed in 3 dimensional hexagonal close packed structure?
View SolutionCalculate the number of octahedral voids of an element having the following arrangement.
(i) Body centred cubic
(ii) Face centred cubic.
View Solutionwhich of the following is not true about the ionic solids ?
(a)Bigger ions form the close packed structure
(b)smaller ions either occupy the tetrahedral or the octahedral voids depending upon their size
(c)Occupation of all voids is not necessary
(d)the fraction of octahedral or tetrahedral voids occupied depends upon the radii of the ions occupying the voids
View Solution
