The density of neon will be minimum at
STP
0∘C,2atm
273∘C,1atm
273∘C,2atm
The correct Answer is:C
To determine the conditions under which the density of neon will be minimum, we can use the ideal gas law and the relationship between density, pressure, and temperature. Here’s a step-by-step solution:
1. Understand the Ideal Gas Law:
The ideal gas law is given by the equation:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the universal gas constant, and T is temperature.
2. Relate Moles to Mass:
The number of moles n can be expressed in terms of mass m and molar mass M:
n=mM
3. Substitute into the Ideal Gas Law:
Substituting n into the ideal gas law gives:
PV=mMRT
4. Express Density:
Density (ρ) is defined as mass per unit volume:
ρ=mV
Rearranging the ideal gas equation to express volume in terms of the other variables:
V=mRTPM
Substituting this into the density equation:
ρ=mmRTP=PMRT
5. Analyze the Density Equation:
From the equation ρ=PMRT, we can see that:
- Density (ρ) is directly proportional to pressure (P).
- Density (ρ) is inversely proportional to temperature (T).
6. Determine Conditions for Minimum Density:
To minimize density, we need to:
- Minimize pressure (P).
- Maximize temperature (T).
7. Identify the Conditions:
Given the options provided in the question (not specified here), select the option where pressure is at its lowest and temperature is at its highest.
8. Conclusion:
The density of neon will be minimum at conditions of low pressure and high temperature.
The ideal gas law is given by the equation:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the universal gas constant, and T is temperature.
The number of moles n can be expressed in terms of mass m and molar mass M:
n=mM
Substituting n into the ideal gas law gives:
PV=mMRT
Density (ρ) is defined as mass per unit volume:
ρ=mV
Rearranging the ideal gas equation to express volume in terms of the other variables:
V=mRTPM
Substituting this into the density equation:
ρ=mmRTP=PMRT
From the equation ρ=PMRT, we can see that:
- Density (ρ) is directly proportional to pressure (P).
- Density (ρ) is inversely proportional to temperature (T).
To minimize density, we need to:
- Minimize pressure (P).
- Maximize temperature (T).
Given the options provided in the question (not specified here), select the option where pressure is at its lowest and temperature is at its highest.
The density of neon will be minimum at conditions of low pressure and high temperature.
Similar Questions
Knowledge Check
A vessel contains two non-reactive gases neon (monoatomic) and oxygen (diatomic). The ratio of their partial pressures is 3:2. Estimate the ratio of
(i) number of molecules, and
(ii) mass density of neon and oxygen in the vessel.
Atomic mass of neon = 20.2 u, and molecular mass of oxygen = 32.0 u.A32B23C13D12In which of the following molecules, π− electron density in ring is minimum ?
A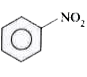 B
B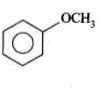 C
C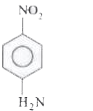 D
D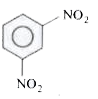
The density of neon gas will be highest at
View SolutionAssertion: A glass of water is filled at 4∘C. Water will overflow, if temperature is increased or decreased. (Ignore expansion of glass).
Reason: Density of water is minimum at 4∘C.
View SolutionA vessel contains two non-reactive gases neon (monoatomic) and oxygen (diatomic). The ratio of their partial pressures is 3:2. Estimate the ratio of
(i) number of molecules, and
(ii) mass density of neon and oxygen in the vessel.
Atomic mass of neon = 20.2 u, and molecular mass of oxygen = 32.0 u.
View SolutionA cylindrical wooden float whose base area S and the height H drift on the water surface. Density of wood d and density of water is ρ. What minimum work must be performed to take the float out of the water ?
View SolutionA wooden stick of length L, radius R and density ρ has a small metal piece of mass m ( of negligible volume) atached to its one end. Find the minimum value for the mass m (in terms of given parameters) that would make the stick float vertically in equilibrium in a liquid of density σ(>ρ).
View SolutionIn which of the following molecules π-electron density in ring is minimum :
View Solution
