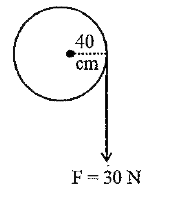
एकं खोखले सिलिन्डर का द्रव्यमान 3 kg तथा त्रिज्या 40 cm है। इस पर एक डोरी लपेट दी गई है। यदि इस डोरी को 30 N के बल द्वारा खींचा जाय तो सिलिन्डर का कोणीय त्वरण किटना होगा
0.25 rad/s2
25 rad/s2
5 m/s2
25 m/s2
The correct Answer is:2
दिया है, सिलिन्डर का द्रव्यमान m = 3kg
R=40 cm=0.4m
F=30N,α=?
हम जानते हैं, आधूर्ण τ=Iα
F×R=MR2α
α=30×(0.4)(3×(0.4))2
या α=25rad/s2
Topper's Solved these Questions
Similar Questions
(μ0ε0)−1/2 की विमा होती है
View Solutionकिसी स्वरित्र द्विभुज का उपयोग किसी ऐसी काँच की नलिका में अन्नुकद उत्पन्न करने के लिया गया है, जिसमे वायु स्तम्भ की लम्बाई को परिवर्ती पिस्टन द्वारा समायोजित किया जा सकता है। 27∘C कक्ष ताप पर स्तम्भ की लम्बाई 20 सेमी और 73 सेमी होने पर दो क्रमागत अनुनाद उत्पन्न होते है। यदि स्वरित्र द्विभुज की आवृत्ति 320 हर्ट्स है, तो वायु में ध्वनि का 27∘C पर वेग है:
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
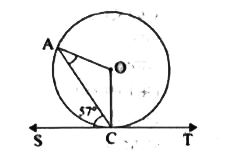
View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
View Solutionएक कम्पनी दो प्रकार के टेलीफोनों का निर्माण करती है|पहला डोरी युक्त,दूसरा डोरी रहित| डोरी युक्त टेलीफ़ोन के निर्माण में 2 घंटे लगते है तथा रहित डोरी मॉडल के निर्माण में 4 घंटे लगते है| कम्पनी के पास इन प्रतिरूपों के निर्माण के लिए प्रतिदिन अधिक से अधिक 800 कार्य घंटे उपलब्ध है तथा पैकिंग विभाग प्रतिदिन अधिक से अधिक 300 टेलीफ़ोन सेटों को पैक कर सकता है|यदि कम्पनी डोरी युक्त मॉडल को रु 300 में बेचती है तथा डोरी रहित मॉडल को रु 400 में बचती है ,तो उसे प्रत्येक प्रकार के कितने टेलीफ़ोन सेल प्रतिदिन निर्मित करने चाहिए जिससे की उसकी बिक्री अधिकतम हो?
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionयदि sinθ=12 तथा θ एक अधिक कोण है , तो cotθ का मान होगा
View Solutionपरवलय y=x2−2x+5 की जीवा दो बिन्दुओं जिनकी कोटि है, x1=1,x2=3 को जोड़ती है, तो इस जीवा के है, को जोड़ती है , तो इस जीवा के समान्तर परवलर की स्पर्श रेखा का समीकरण होगा
View Solutionयदि बिंदु (3,4) समीकरण 3y=ax+6 के आलेख पर स्थित है , तो a का मान होगा :
View Solutionएक समतल निर्देशाक्षों को क्रमश: A, B तथा C पर काटता है। यदि △ABC का केन्द्रक (2,-1, 3) है, तो समतल का समीकरण ज्ञात कीजिए।
View Solution
