R त्रिज्या और m द्रव्यमान वाली एक समान वृत्ताकार डिस्क का अपनी तल के लम्बवत तथा किनारे से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण है : -
MR2
12MR2
32MR2
72MR2
The correct Answer is:C
R त्रिज्या M और द्रव्यमान वाली डिक्स के केंद्र से निकलने वाले लम्बवत अक्ष के परितः डिस्क का जड़त्व है :
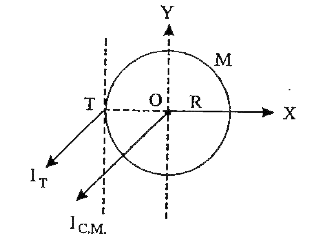
IC.M.=12MR2
समांतर -अक्ष प्रमेय से
IT=IC.M+MR2
=12MR2+MR2=32MR2
Topper's Solved these Questions
Similar Questions
ऊष्मागतिकी का प्रथम नियम किसके संरक्षण पर आधारित है।
09:03View Solutionतीन पिण्ड a : ( एक ठोस गोला ), b : ( एक पतली वृत्ताकार चकती ) तथा c : ( एक वृत्ताकार छल्ला ), जिनमें प्रत्येक का द्रव्यमान m तथा त्रिज्या r हैं, समान कोणीय चाल से अपनी सममिति अक्षों के परितः चक्रण कर रहे हैं | इन्हें विरामावस्था में लाने के लिए किए जाने वाले आवश्यक कार्यों ( w ) के लिए कौन - सा सम्बन्ध सही है ?
03:10View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?06:22View Solutionएक रेखा के कार्तीय समीकरण 6x−2=3y+1=2z−2 है। रेखा के दिक्-अनुपात ज्ञात कीजिए तथा बिन्दु (2,−1,−1) से गुजरने वाली उस रेखा का सदिश समीकरण लिखिए जो दी हुई रेखा के समान्तर है।
01:28View Solution'अ' 'ब' 1.जूल×सेकण्ड(i) आयताकार पटल का जड़त्व आघूर्ण2. [ML2T−1](ii) 25MR23. जड़त्व आघूर्ण(iii) कोणीय संवेग4. I=M(l2+b212)(iv) घूर्णन गति5. एक ठोस गोला ( द्रव्यमान M, त्रिज्या(v) कोणीय संवेग का विमीय सूत्र R ) व्यास के परितः जड़त्व आघूर्ण
01:21View Solutionबिंदु (5,7,9) से गुजरने वाली उन सरल रेखाओ के समीकरण ज्ञात कीजिए, जो निम्न अक्षो, के समांतर है :
X-अक्ष04:32View Solutionबिंदु (5,7,9) से गुजरने वाली उन सरल रेखाओ के समीकरण ज्ञात कीजिए, जो निम्न अक्षो, के समांतर है :
Y-अक्ष04:26View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
02:42View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
04:27View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
02:27View Solutionबिंदु hati + 2hatj- hatk से गुजरने वाले तथा hati + 2hatj + hatk से निरूपित बल का बिंदु 2hati + 3hatj + hatk के परितः सदिश आघूर्ण ज्ञात कीजिए|
53:48View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
49:03View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष तथा केन्द्र पर चुंबकीय क्षेत्र | ऐम्पियर का परिपथीय नियम
39:43View Solutionधारावाही वृत्ताकार लूप और कुंडली के अक्ष पर चुंबकीय क्षेत्र
View Solutionगति के प्रथम नियम |जड़त्व तथा द्रव्यमान |OMR|Summary
View Solution1.0 mg के द्रव्यमान वाले एक कण का वेग 3600 km/h है। कण के तरंग दैर्ध्य की गणना कीजिए।
View Solution

