Question

सिद्ध कीजिए :
यदि एक चतुर्भुज में सम्मुख कोणों का प्रत्येक युग्म बराबर हो तो वह चतुर्भुज समान्तर चतुर्भुज होता है।

Explanation

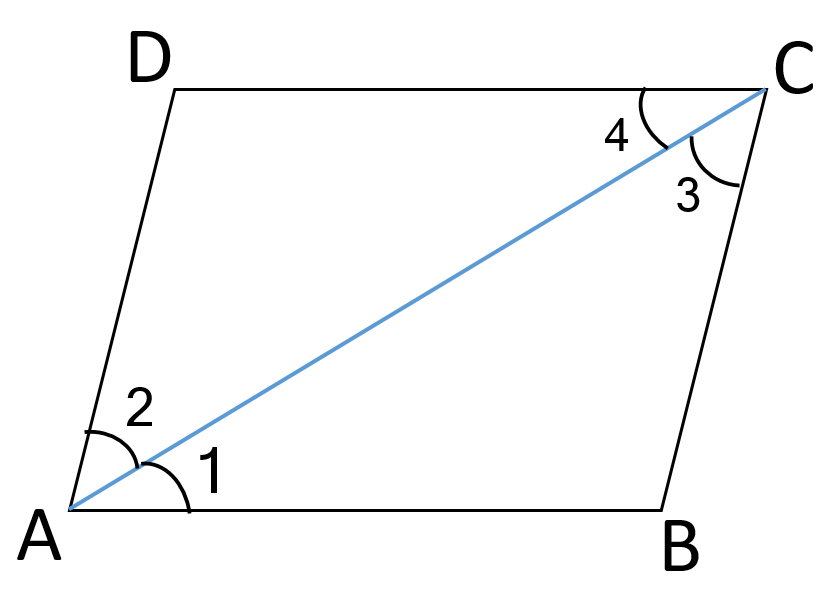
जैसा कि दिया गया है, मान लिया कि ABCD एक चतुर्भुज है। और इसकी सम्मुख भुजाएँ AD `=` BC और AB` = `DC

सिद्ध करना है कि ABCD एक समांतर चतुर्भुज.



अत: चतुर्भुज का विकर्ण PR खींचा गया।

`triangleACD` और `triangleABC` में, AD `=` BC [जैसा कि दिया गया है]

और, AB` =` DC [जैसा कि दिया गया है]

और भुजा AC दोनों त्रिभुजों में उभयनिष्ठ (कॉमन) है।

अत: By SSS (भुजा भुजा भुजा) सर्वांगसमता नियम से

ΔACD ≅ ΔABC

अत: CPCT के अनुसार हम जानते हैं कि सर्वांगसम त्रिभुजों मे संगत भाग बराबर होते हैं

अत: `angle1 = angle4`

और, `angle3 = angle2`

अब समांतर रेखाओं के एक प्रमेय से हम जानते हैं कि जो कहता है यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार काटे कि एकांतर अंत: कोणों का प्रत्येक युग्म बराबर हों, तो रेखाएँ समांतर होती हैं।

यहाँ तिर्यक रेखा AC दिये गये दो रेखाओं AD और BC को इस प्रकार काटती है कि एकांतर अंत: कोणों का युग्म `angle1` और `angle4` तथा `angle3` और `angle2` बराबर हैं।

अत: AD||BC और AB||DC

चूँकि दिये गये चतुर्भुज में सम्मुख भुजाएँ समांतर हैं, अत: PQRS एक समांतर चतुर्भुज है।प्रमाणित

अत: यदि एक चतुर्भुज की सम्मुख भुजाओं का प्रत्येक युग्म बराबर हो, तो वह एक समांतर चतुर्भुज होता है।