सिद्ध कीजिए :
समांतर चतुर्भुज के विकर्ण एक दूसरे को (परस्पर) समद्विभाजित करते है।
वीडियो समाधान
लिखित उत्तर
जैसा कि दिया गया है, मान लिया कि ABCD एक समांतर चतुर्भुज हैं और, AC और DB इस चतुर्भुज के दो विकर्ण हैं।
अत: सिद्ध करना है कि AC और DB एक दूसरे को समद्विभाजित करते हैं।
अर्थात OA = OR और OB=OD
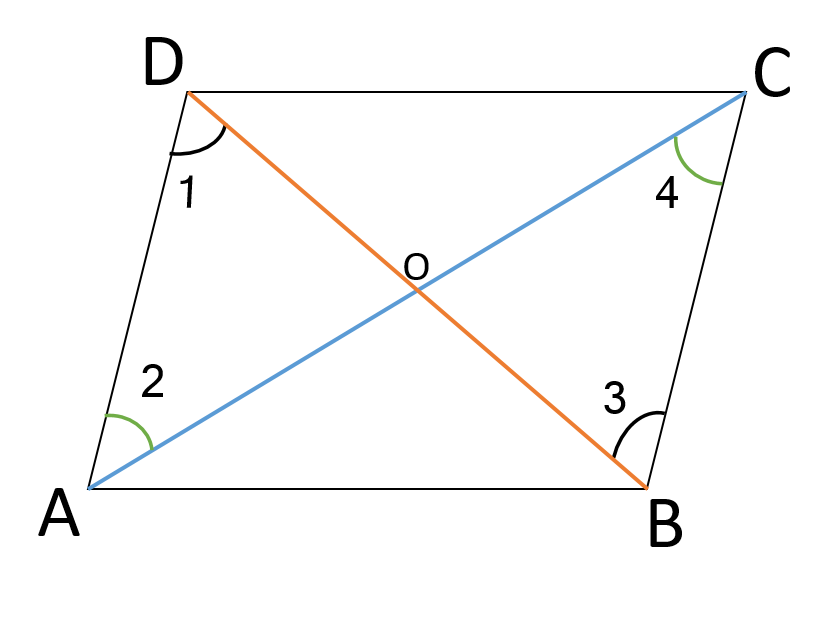
चूँकि ABCD एक समांतर चतुर्भुज है,
अत: AD =BC और AD||BC
अब △AOD और △BOC में,
AD||BC और एक तिर्यक रेखा AC इन्हें काटती है, अत: एकांतर अंत: कोणों का प्रत्येक युग्म आपस में बराबर होंगे।
अत: ∠2=∠4 - - - - - (i)
उसी प्रकार, AD||BC और एक तिर्यक रेखा BD इन्हें काटती हैं, अत: एकांतर अंत: कोणों का प्रत्येक युग्म बराबर होंगे।
अत: ∠1=∠3 - - - - (ii)
और, AD = BC [चूँकि समांतर चतुर्भुज की सम्मुख भुजाएँ हैं।]
अत: ASA (कोण भुजा कोण) सर्वांगसमता नियम से,
△AOD≅△BOC
अब CPCT नियम से हम जानते हैं कि सर्वांगसम त्रिभुजों मे संगत भाग बराबर होते हैं,
अत: OA=OC और OD = OB
अत: समांतर चतुर्भुज के विकर्ण एक दूसरे को (परस्पर) समद्विभाजित करते हैं। प्रमाणित

|
Updated on:21/07/2023
समान प्रश्न
चतुर्भुज |चतुर्भुज का कोण योग गुण |चतुर्भुज के प्रकार |समांतर चतुर्भुज के गुण|प्रमेय|सारांश
51:39View Solutionसमांतर चतुर्भुज के गुण
29:12View Solutionएक ही आधार और एक ही समांतर रेखाओं के बीच आकार्तियाँ#!#एक ही आधार और एक ही समांतर रेखाओ के बीच समांतर चतुर्भुज
31:37View Solutionसमांतर चतुर्भुज के कोण
36:27View Solutionसमांतर चतुर्भुज के विकर्ण
34:53View Solutionदोहरान | चतुर्भुजों के प्रकार |समांतर चतुर्भुजों के अवयव |समांतर चतुर्भुजों के कोण |समांतर चतुर्भुजों के विकर्ण |सारांश
43:04View SolutionIf ABCD is a cyclic parallelogram , then the ∠A is .
यदि ABCD एक चक्रीय समांतर चतुर्भुज है, तो ∠A क्या है?01:56View Solutionसमांतर चतुर्भुज के गुण
49:42View Solution

