In △ABC, AB=7 cm, BC = 10 cm, and AC = 8 cm. If AD is the angle bisector of ∠BAC , where D is a point on BC, then BD is equal to:
163 cm
143 cm
174cm
154 cm
To find the length of segment BD in triangle ABC where AD is the angle bisector of angle BAC, we can use the Angle Bisector Theorem. This theorem states that the ratio of the lengths of the two segments created by the angle bisector on the opposite side is equal to the ratio of the lengths of the other two sides of the triangle.
1. Identify the lengths of the sides of the triangle:
- AB = 7 cm
- AC = 8 cm
- BC = 10 cm
2. Let BD = x.
- Then, since D is on BC, we have CD = BC - BD = 10 - x.
3. Apply the Angle Bisector Theorem:
According to the theorem:
ABAC=BDCD
Substituting the known lengths:
78=x10−x
4. Cross-multiply to solve for x:
7(10−x)=8x
Expanding the left side:
70−7x=8x
5. Combine like terms:
70=8x+7x
70=15x
6. Solve for x:
x=7015=143
7. Conclusion:
Thus, the length of segment BD is:
BD=143 cm
- AB = 7 cm
- AC = 8 cm
- BC = 10 cm
- Then, since D is on BC, we have CD = BC - BD = 10 - x.
According to the theorem:
ABAC=BDCD
Substituting the known lengths:
78=x10−x
7(10−x)=8x
Expanding the left side:
70−7x=8x
70=8x+7x
70=15x
x=7015=143
Thus, the length of segment BD is:
BD=143 cm
Topper's Solved these Questions
Similar Questions
In △ABC AB = 7 cm, BC =10cm, and AC = 8 cm. If AD is the angle bisector of ∠BAC, where D is a point on BC, then BD is equal to:
यदि त्रिभुज ABC में, AB = 7 सेमी, BC = 10 सेमी तथा AC =8 सेमी है | यदि AD कोण BAC का समद्विभाजक है, जहाँ D, BC पर स्थित एक बिंदु है, तो BD का मान किसके बराबर है ?
View SolutionIn triangle ABC, AB = 6, AC = 7 and BC = 8. If AD is bisector of angleA , then find the length of BD and CD.
View Solution
Knowledge Check
In a △ABC. AB = 5 cm, AC = 7 cm. If AD is the angle bisector of angle A, then BD :CD is :
A25:49B49:25C6:1D5:7In △ABC,AB=6cm,AC=8cm,andBC=9cm. The length of median AD is :
A√3172cmB√1192cmC√1152cmD√3132cmIn Δ ABC, AB = 6 cms, BC = 10 cms, AC = 8cm and ADI_BC. Find the value of the ratio of BD:DC.
A3:4B9:16C4:5D16:25
In △ABC, AB = 6 cm, AC = 8 cm, and BC = 9 cm. The length of median AD is:
View SolutionIn a ΔABC,∠A=120∘,AB=20cm,AC=30cm find the angle bisector AD .
View SolutionIn ΔABC,AB=12cm,BC=16cm and CA=20cm If D is the mid point of AC then the length of BD is
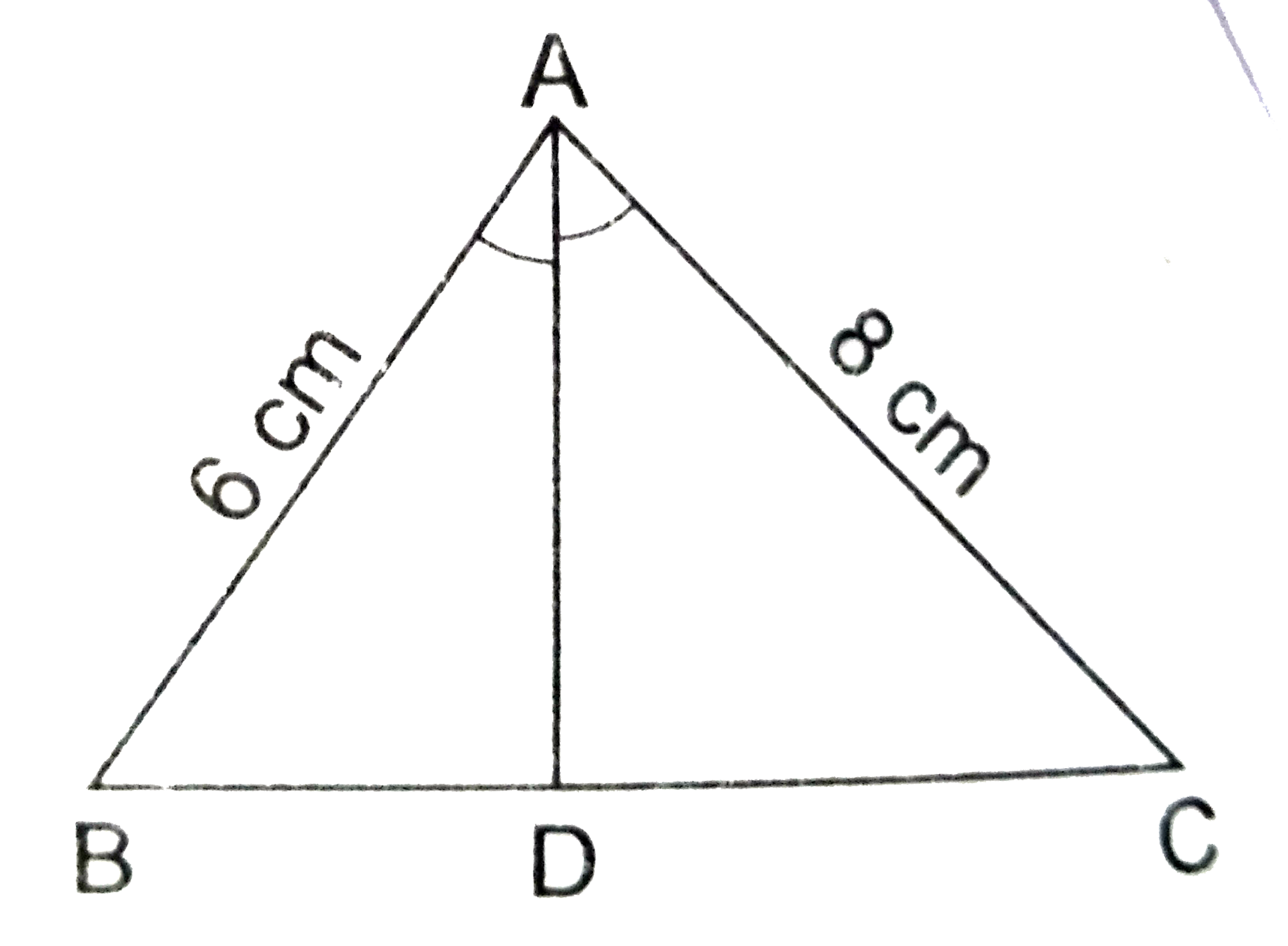
View SolutionIn aΔABC it is given that AB=6cm,AC=8cmandAD is the bisector of ∠A. Then BD:DC=?
View SolutionIn ΔABC, AB=6√3cm, AC=12cm and BC=6cm. Then ∠B is
View Solution
