ഒരു അർധവൃത്തത്തിലെ ഒരു ബിന്ദുവും, വ്യാസത്തിന്റെ രണ്ടറ്റങ്ങളും ചേർന്ന് ഒരു ത്രികോണം വരച്ചു തുടർന്ന്, ത്രികോണത്തിന്റെ മറ്റു രണ്ട് വ്സങ്ങൾ വ്യാസം ആയി അർധവൃത്തങ്ങളും വരച്ചു. രണ്ടാം ചിത്രത്തിലെ നീലയും ചുവപ്പുമായ ചന്ദ്രക്കലകളുടെ പരപ്പളവ് കൂട്ടിയാൽ ത്രികോണത്തിന്റെ പരപ്പളവ് കിട്ടുമെന്ന് തെളിയിക്കുക .
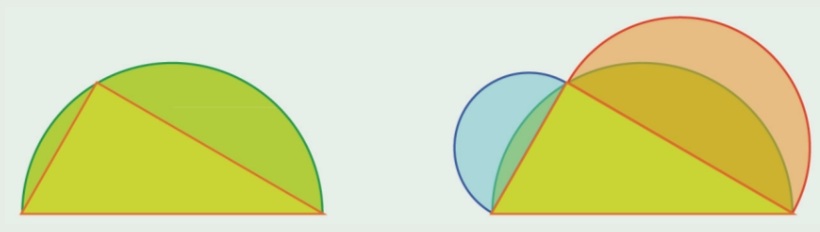
Step by step video & image solution for ഒരു അർധവൃത്തത്തിലെ ഒരു ബിന്ദുവും, വ്യാസത്തിന്റെ രണ്ടറ്റങ്ങളും ചേർന്ന് ഒരു ത്രികോണം വരച്ചു തുടർന്ന്, ത്രികോണത്തിന്റെ മറ്റു രണ്ട് വ്സങ്ങൾ വ്യാസം ആയി അർധവൃത്തങ്ങളും വരച്ചു. രണ്ടാം ചിത്രത്തിലെ നീലയും ചുവപ്പുമായ ചന്ദ്രക്കലകളുടെ പരപ്പളവ് കൂട്ടിയാൽ ത്രികോണത്തിന്റെ പരപ്പളവ് കിട്ടുമെന്ന് തെളിയിക്കുക . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
The inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View Solutionഒരു സമഭുജ ത്രികോണത്തിൻറെ പരിവൃത്ത കേന്ദ്രം, അതിൻറെ മധ്യമകേന്ദ്രം തന്നെയാണെന്ന് തെളിയിക്കുക. വ്യാസം ഒരു സെൻറീമീറ്ററായ വൃത്തത്തിലെ 3 ബിന്ദുക്കൾ യോജിപ്പിച്ചുണ്ടാക്കുന്ന സമഭുജത്രികോണത്തിൻറെ ഒരു വശത്തിൻറെ നീളം കാണുക.
View Solutionഒരു സമചതുരത്തിനുള്ളിൽ ചിത്രത്തിൽ കാണുന്നതുപോലെ വൃത്തഭാഗങ്ങൾ വരയ്ക്കുന്നു. ചിത്രത്തിലെ കറുപ്പിച്ചിരിക്കുന്ന ഭാഗത്തിന്റെ പരപ്പളവ് സമചതുരത്തിന്റെ പരപ്പളവിന്റെ പകുതിയാണെന്ന് തെളിയിക്കുക.
View Solutionഒരു സമഭുജത്രികോണത്തിൻറെ ഓരോ മൂലയും കേന്ദ്രമായി മറ്റു രണ്ടു മൂലകളിൽ കൂടി കടന്നുപോകുന്ന വൃത്തം വരച്ച ചിത്രമാണ് തന്നിരിക്കുന്നത്. 3 വൃത്തങ്ങളിലും ഉൾപ്പെടുന്ന ഭാഗത്തിന്റെ പരപ്പളവ് കണക്കാക്കുക.
View Solutionചിത്രത്തിൽ ഒരു ഇരുമ്പു ബോൾട്ടിന്റെ ഒരു അഗ്ര മുഖമാണ്. ഉള്ളിലെ വൃത്തത്തിന്റെ ആരം 1 സെ.മീ ഉം കേന്ദ്രത്തിൽ സമഷട്ഭുജത്തിൻറെ ഒരു വശം 1.5 സെ.മീറ്ററുമാണ്. ചിത്രത്തിലെ കറുപ്പിച്ച ഭാഗത്തിന്റെ പരപ്പളവ് കാണുക.
View Solution4 സെൻറീമീറ്റർ വശമുള്ള ഒരു സമഭുജ ത്രികോണത്തിന്റെ മൂലകളിൽ നിന്നും വശത്തിന്റെ പകുതി വ്യാസമായി വൃത്തം വരച്ചിരിക്കുന്നു. ചിത്രത്തിലെ കറുപ്പിച്ച ഭാഗത്തിന്റെ പരപ്പളവ് കാണുക.
View Solution
