Find the equivalent definition of f(x)=max{x2,(1−x)2,2x(1−x)}where 0≤x≤1Solution in Bengali
Here, for maximum, let us consider f1(x)=x2,f2(x)=(1−x)2, and f3(x)=2x(1−x).
Now graph for f1(x),f2(x), and f3(x) are as follows.
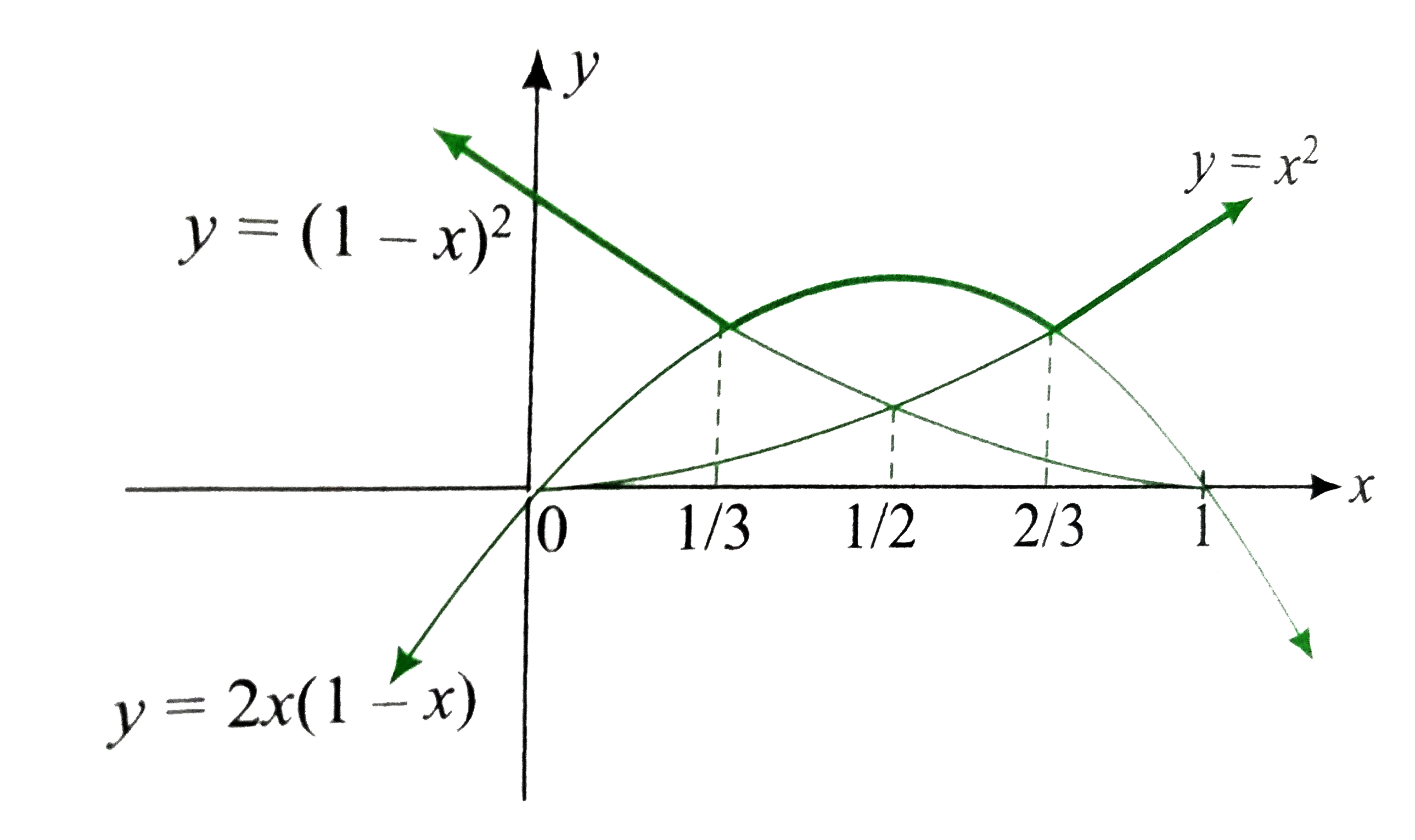
Here, neglect the graph that is below the points of intersection.
f(x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩(1−x)2,0≤x<132x(1−x),13≤x<23x2,23≤x≤1
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 6
View SolutionIf f(x)=maξμm{x3,x2,164}∀x∈[0,∞),then f(x)={x2,0≤x≤1x3,x>0 f(x)={164,0≤x≤14x2,14<x≤1x3,x>1 f(x)={164,0≤x≤18x2,18<x≤1x3,x>1 f(x)={164,0≤x≤18x3,x>18
View SolutionLet f(x)=M a xi mu m{x2,(1−x)2,2x(1−x)}, where 0≤x≤1. Determine the area of the region bounded by the curves y=f(x),x-axis ,x=0,andx=1.
View SolutionFind the greatest and least values of function f(x)={−x, −1≤x<02−(x−1)2, 0≤x≤2
View SolutionThe points of discontinuity of the function f(x)={2√x , 0≤x≤1, 4−2x , 1<x
View SolutionIf f:[0,3]→[0,3] is defined by:
f(x)={1+x0≤x≤23−x2<x≤3 , then show that f[0,3]⊆[0,3] and find fof.
View SolutionFind (lim)x→1f(x) ,where f(x)={x2−1x≤1−x2−1x>1
View SolutionFind the equivalent definition of f(x)=max{x2,(1−x)2,2x(1−x)}where 0≤x≤1
View SolutionIf f(x)=max{x3,x2,164}∀x∈[0,∞),then f(x)={x2,0≤x≤1x3,x>0 f(x)={164,0≤x<=14x2,14<x≤1x3,x>1 f(x)={164,0≤x≤18x2,18<x≤1x3,x>1 f(x)={164,0≤x≤18x3,x>18
View SolutionIn the hexaploid wheat, the haploid (n) and basic (x) numbers of chromosomes are
View SolutionFind the equivalent definition of f(x)=max.x2,(−x)2,2x(1−x)where0≤x≤1
View SolutionMaximum value of x(1−x)2 when 0≤x≤2 is
View SolutionFind the equivalent definition of f(x)=max{x2,(1−x)2,2x(1−x)}where 0≤x≤1
View SolutionIf f(x)=maξμm{x3,x2,164}∀x∈[0,∞),then f(x)={x2,0≤x≤1x3,x>0 f(x)={164,0≤x≤14x2,14<x≤1x3,x>1 f(x)={164,0≤x≤18x2,18<x≤1x3,x>1 f(x)={164,0≤x≤18x3,x>18
View SolutionLet f(x) =M a xi mu m {x^2,(1-x)^2,2x(1-x)}, where 0lt=xlt=1. Determine the area of the region bounded by the curves y=f(x) ,x-axis ,x=0, and x=1.
View Solution
