[Bengali] If a x ^2+b x+c=0 has imaginary roots and a-b+c >0 then the

Prove that ${(.^{2 n} C_{0})}_{0}^{2} - {(.^{2 n} C_{1})}_{1}^{2} + {(.^{2 n} C_{2})}_{2}^{2} - . . + {(.^{2 n} C_{2 n})}_{2 n}^{2}$ = ${(- 1)}^{n} .^{2 n} C_{n}$ .

View Solution

Let $A (0, 1), B (1, 1), C (1, - 1), D (- 1, 0)$ be four points. If P is any other point, then $P A + P B + P C + P D \geq d$ , when $[d]$ is where $[.]$ represents greatest integer.

View Solution

Solve the following pair of linear equations:
(i) $p x + q y = p q; q x p y = p + q$
(ii) $a x + b y = c; b x + a y = 1 + c$
(iii) $\frac{x}{a} - \frac{y}{b} = 0$ ; $a x + b y = a^{2} + b^{2}$
(iv) $(a - b) x + (a + b) y = a^{2} - 2 a b - b^{2};$ $(a + b) (x + y) = a^{2} + b^{2}$
(v) 152x − 378y = − 74; 76x − 189y = − 37

View Solution

If $a x^{2} + b x + c = 0$ has imaginary roots and $a - b + c > 0$ then the set of points $(x, y)$ satisfying the equation $∣ ∣ a (x^{2} + \frac{y}{a}) + (b + 1) x + c ∣ ∣ = ∣ ∣ a x^{2} + b x + c ∣ ∣ + | x + y |$ consists of the region in the $x y - p l a n e$ which is on or above the bisector of I and III quadrant on or above the bisector of II and IV quadrant on or below the bisector of I and III quadrant on or below the bisector of II and IV quadrant

View Solution

The equation of the bisector of the acute angle between the lines $2 x - y + 4 = 0$ and $x - 2 y = 1$ is (a) $x - y + 5 = 0$ (b) $x - y + 1 = 0$ (c) $x - y = 5$ (d) none of these

View Solution

Let $A B C$ be a triangle. Let $A$ be the point $(1, 2), y = x$ be the perpendicular bisector of $A B,$ and $x - 2 y + 1 = 0$ be the angle bisector of $∠ C$ . If the equation of $B C$ is given by $a x + b y - 5 = 0$ , then the value of $a + b$ is (a) $1$ (b) $2$ (c) $3$ (d) $4$

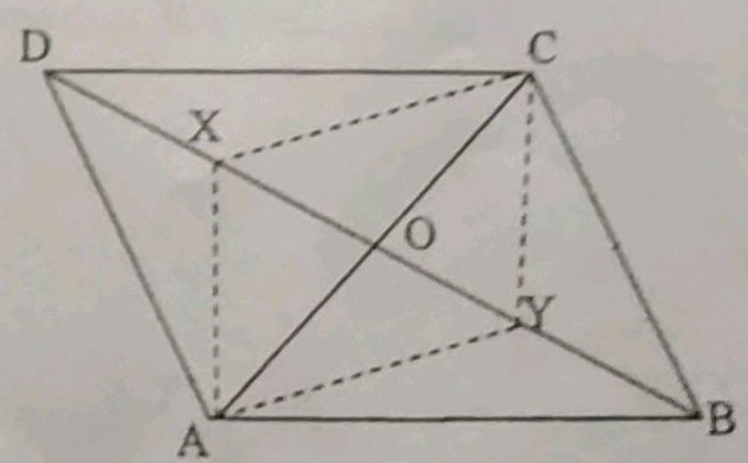
View Solution

In Figure, $A B C D$ is a parallelogram and $X a n d Y$ are points on the diagonal $B D$ such that $D X = B Y$ . Prove that $A X C Y$ is a parallelogram (ii) $A X = C Y, A Y = C X$ $A Y B ≅ C X D$ (iv) $A X D ≅ C Y B$
ocr_image

View Solution

Evaluate each of the following algebraic expressions for $x = 1, y = - 1, z = 2, a = - 2, b = 1, c = - 2 :$ (i) $a x + b y + c z$ (ii) $a x^{2} + b y^{2} - c z^{2}$ (iii) $a x y + b y z + c x y$

View Solution

If (a+b+c)>0 and a < 0 < b < c, then the equation a(x-b)(x-c)+b(x-c)(x-a)+c(x-a)(x-c)=0 has (i) roots are real and distinct (ii) roots are imaginary (iii) product of roots are negative (iv) product of roots are positive

View Solution

If 2x+y-4=0 is bisector of the angle between the lines a(x-1)+b(y-2)=0,c(x-1)+d(y-2)=0 then other bisector is

View Solution

If $a x^{2} + b x + c = 0$ has imaginary roots and a - b + c $>$ 0 .
then the set of point (x, y) satisfying the equation
$∣ ∣ a (x^{2} + \frac{y}{a}) + (b + 1) x + c ∣ ∣ = ∣ ∣ a x^{2} + b x + c ∣ ∣ + | x + y |$
of the region in the xy- plane which is

View Solution

Prove that.
(i) $\sqrt{x^{- 1} y} . \sqrt{y^{- 1} z} . S q r t (z^{- 1} x) = 1$
(ii) ${(\frac{1}{x^{a - b}})}^{\frac{1}{a - c}} . (\frac{1}{x^{b - c}}) . {(\frac{1}{x^{c - b}})}^{\frac{1}{c - b}} = 1$
(iii) $\frac{x^{a (b - c)}}{x^{b (a - c)}} \div (\frac{x^{b}}{x^{a}})$ (iv) $\frac{{(x^{a + b})}^{2} {(x^{b + c})}^{2} {(x^{c + a})}^{2}}{{(x^{a} x^{b} x^{c})}^{4}}$

View Solution

If $a x^{2} + b x + c = 0$ has imaginary roots and $a - b + c > 0$ then the set of points $(x, y)$ satisfying the equation $∣ ∣ a (x^{2} + \frac{y}{a}) + (b + 1) x + c ∣ ∣ = ∣ ∣ a x^{2} + b x + c ∣ ∣ + | x + y |$ consists of the region in the $x y - p l a n e$ which is on or above the bisector of I and III quadrant on or above the bisector of II and IV quadrant on or below the bisector of I and III quadrant on or below the bisector of II and IV quadrant

View Solution

Let $A B C$ be a triangle. Let $A$ be the point $(1, 2), y = x$ be the perpendicular bisector of $A B,$ and $x - 2 y + 1 = 0$ be the angle bisector of $∠ C$ . If the equation of $B C$ is given by $a x + b y - 5 = 0$ , then the value of $a + b$ is (a) $1$ (b) $2$ (c) $3$ (d) $4$

View Solution

In Figure, $A B C D$ is a parallelogram and $X a n d Y$ are points on the diagonal $B D$ such that $D X = B Y$ . Prove that $A X C Y$ is a parallelogram (ii) $A X = C Y, A Y = C X$ $A Y B ≅ C X D$ (iv) $A X D ≅ C Y B$

View Solution

Evaluate each of the following algebraic expressions for $x = 1, y = - 1, z = 2, a = - 2, b = 1, c = - 2 :$
(i) $a x + b y + c z$
(ii) $a x^{2} + b y^{2} - c z^{2}$
(iii) $a x y + b y z + c x y$

View Solution

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-COMPLEX NUMBERS AND QUADRATIC EQUATIONS-All Questions