Prove that the locus of midpoint of line segment intercepted between real and imaginary axes by the line az+az+b=0,whereb is a real parameterand a is a fixed complex number with nondzero real and imaginary parts, is az+az=0.Solution in Bengali
Step by step video & image solution for Prove that the locus of midpoint of line segment intercepted between real and imaginary axes by the line a z + a z+b=0,w h e r eb is a real parameterand a is a fixed complex number with nondzero real and imaginary parts, is a z+ a z =0. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Prove that (.2nC0)2−(.2nC1)2+(.2nC2)2−..+(.2nC2n)2 = (−1)n.2nCn.
View SolutionLet A(0,1),B(1,1),C(1,−1),D(−1,0) be four points. If P is any other point, then PA+PB+PC+PD≥d, when [d] is where [.] represents greatest integer.
View SolutionIf z=1+ithenz10 reduces to: A purely imaginary number An imaginary number A purely real number A complex number
View SolutionIf z is a unimodular number (≠±i) then z+iz−i is (A) purely real (B) purely imaginary (C) an imaginary number which is not purely imaginary (D) both purely real and purely imaginary
View SolutionIf z=∣∣ ∣∣1+i5+2i3−2i7i−3i5i1−i5−2i3+2i∣∣ ∣∣ then (A) z is purely real imaginary (B) z is purely real (C) z has equal real and imaginary parts (D) z has positive real and imaginary parts.
View SolutionThe complex number z is is such that |z|=1,z≠−1andw=z−1z+1. Then real part of w is-
View SolutionThe complex number z is such that |z|=1, z≠−1 and w=z−1z+1. Then real part of w is
View SolutionLet z be a complex number such that the imaginary part of z is nonzero and a=z2+z+1 is real. Then a cannot take the value
View SolutionProve that the locus of midpoint of line segment intercepted between real and imaginary axes by the line az+az+b=0,whereb is a real parameterand a is a fixed complex number with nondzero real and imaginary parts, is az+az=0.
View SolutionLet z=9+bi,whereb is nonzero real and i2=−1. If the imaginary part of z2andz3 are equal, then b3 is ______.
View SolutionLet z=9+bi,whereb is nonzero real and i2=−1. If the imaginary part of z2andz3 are equal, then b/3 is ______.
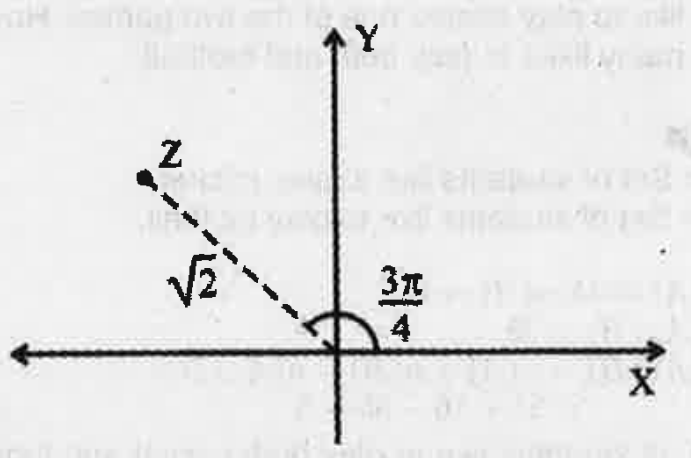
View SolutionIn the above figure , Z represents a complex number.
Find real and imaginary parts of Z.
View SolutionLet z be a complex number such that the imaginary part of z is nonzero and a = z^2 + z + 1 is real. Then a cannot take the value
View SolutionIf z is a unimodular number (≠±i) then z+iz−i is (A) purely real (B) purely imaginary (C) an imaginary number which is not purely imaginary (D) both purely real and purely imaginary
View SolutionLet z be a complex number such that the imaginary part of z is nonzero and a=z2+z+1 is real. Then a cannot take the value
View SolutionProve that the locus of midpoint of line segment intercepted between real and imaginary axes by the line ¯az+a¯z+b=0,whereb is a real parameterand a is a fixed complex number with nondzero real and imaginary parts, is az+¯a¯z=0.
View Solution
