The three angular points of a triangle are given by Z=α,Z=β,Z=γ,whereα,β,γ are complex numbers, then prove that the perpendicular from the angular point Z=α to the opposite side is given by the equation Re(Z−αβ−γ)=0Solution in Bengali
Step by step video & image solution for The three angular points of a triangle are given by Z=alpha, Z=beta,Z=gamma,w h e r ealpha,beta,gamma are complex numbers, then prove that the perpendicular from the angular point Z=alpha to the opposite side is given by the equation R e((Z-alpha)/(beta-gamma))=0 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Prove that (.2nC0)2−(.2nC1)2+(.2nC2)2−..+(.2nC2n)2 = (−1)n.2nCn.
View SolutionLet A(0,1),B(1,1),C(1,−1),D(−1,0) be four points. If P is any other point, then PA+PB+PC+PD≥d, when [d] is where [.] represents greatest integer.
View SolutionIf alpha,beta,gamma are cube roots of of p<0 then for any real x,y,z;(x alpha+y beta+z gamma)/(x beta+y gamma+z alpha)=
View SolutionThe three angular points of a triangle are given by Z=α,Z=β,Z=γ,whereα,β,γ are complex numbers, then prove that the perpendicular from the angular point Z=α to the opposite side is given by the equation Re(Z−αβ−γ)=0
View SolutionIf α,β,γ are the angles of a triangle and system of equations cos(α−β)x+cos(β−γ)y+cos(γ−α)z=0 cos(α+β)x+cos(β+γ)y+cos(γ+α)z=0 sin(α+β)x+sin(β+γ)y+sin(γ+α)z=0 has non-trivial solutions, then triangle is necessarily a. equilateral b. isosceles c. right angled d. acute angled
View SolutionIf alpha,beta,gamma,delta are four complex numbers such that (gamma)/(delta) is real and alpha delta-beta gamma!=0 then z=(alpha+beta t)/(gamma+delta t) represents a
View SolutionIf =(beta-gamma)(alpha-delta),y=(gamma-alpha)(beta-delta),z=(alpha-beta)(gamma-delta) ,then value of x^(3)+y^(3)+z^(3)-3xyz is
View SolutionThree vertices of triangle are complex number α,β and γ. Then prove that the perpendicular form the point α to opposite side is given by the equation Re(z−αβ−γ)=0 where z is complex number of any point on the perpendicular.
View SolutionLet P(α,β,γ)andQ(1,−1,0) be points such that the mid-point of PQ is R(x,y,z). If x is the AM of αandβ,y is the G.M. of βandγandz is the H.M . Of γandα then :
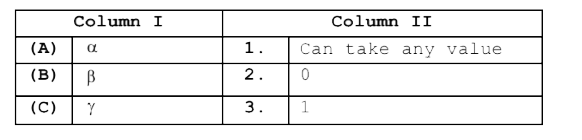
View SolutionIf α,β,γ are the cube roots of a negative number p, then for any three real numbers x,y,z the value of xα+yβ+zγxβ+yγ+zα is
View SolutionThe three angular points of a triangle are given by Z=α,Z=β,Z=γ,whereα,β,γ are complex numbers, then prove that the perpendicular from the angular point Z=α to the opposite side is given by the equation Re(Z−αβ−γ)=0
View SolutionIf α,β,γ,δ are four complex numbers such that γδ is real and αδ−βγ≠0 then z = α+βtγ+δt where t is a rational number, then it represents:
View SolutionIf α,β,γ are the angles of a triangle and system of equations cos(α−β)x+cos(β−γ)y+cos(γ−α)z=0 cos(α+β)x+cos(β+γ)y+cos(γ+α)z=0 sin(α+β)x+sin(β+γ)y+sin(γ+α)z=0 has non-trivial solutions, then triangle is necessarily a. equilateral b. isosceles c. right angled d. acute angled
View SolutionLet P(α,β,γ)andQ(1,−1,0) be points such that the mid-point of PQ is R(x,y,z). If x is the AM of αandβ,y is the G.M. of βandγandz is the H.M . Of γandα then :
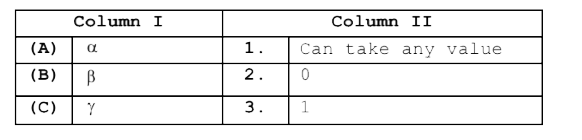
View SolutionProve that
∣∣ ∣ ∣∣1x+αy+z−α1y+βz+x−β1z+γx+y−γ∣∣ ∣ ∣∣=0
View Solution
