Match the value of x in column II where derivative of the function in column I is negative. Column I Column II y=∣∣x2−2∣∣x∣∣∣ p. (1,2) y=∣∣(log)e∣∣x∣∣∣ q. (−3,−2) y=x[x2],where[.] represent r. (−1,0) y=|sinx| s. (0,1)Solution in Bengali
Step by step video & image solution for Match the value of x in column II where derivative of the function in column I is negative. Column I Column II y=|x^2-2|x|| p. (1,2) y=|(log)_e|x|| q. (-3,-2) y=x[x/2],w h e r e[dot] represent r. (-1,0) y=|sinx| s. (0,1) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
- LINEAR INEQUALITIESBOOK - CENGAGE PUBLICATIONCHAPTER - LINEAR INEQUALITIESEXERCISE - All Questions
68 Videos
Similar Questions
Let →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆk and →c=c1ˆi+c2ˆj+c3ˆk be three non- zero vectors such that →c is a unit vectors perpendicular to both the vectors →a and →b. If the angle between →a and →b is π6 then
∣∣ ∣∣a1a2a3b1b2b3c1c2c3∣∣ ∣∣2 is equal to
View SolutionSolve |x|+|x−2|=2.
View SolutionMatch the graph of y = f(x) in Column I with the corresponding graph of y = f'(x) in Column II.
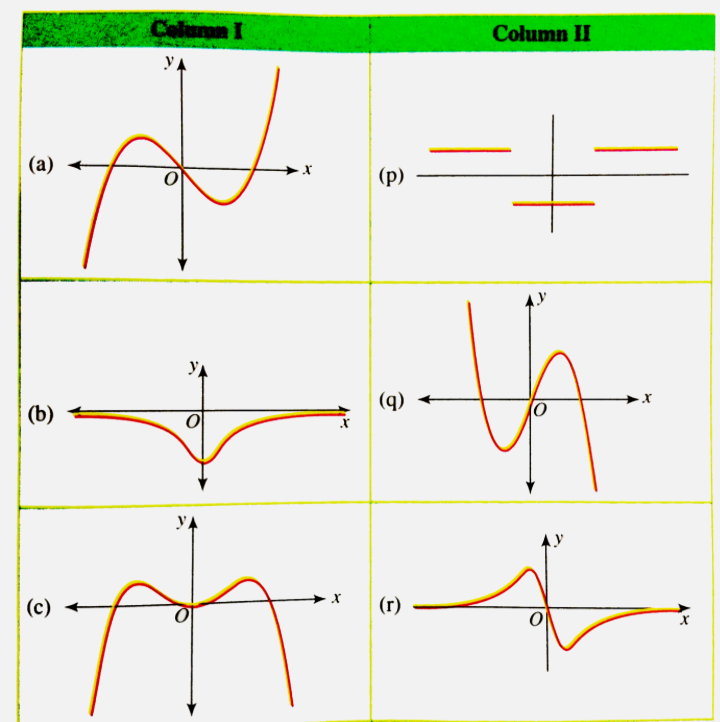
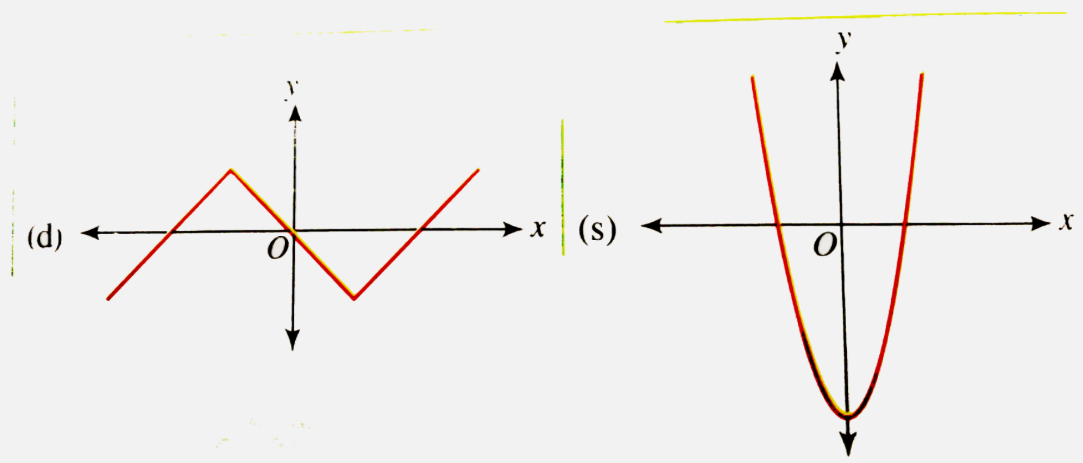
View SolutionColumn Ax=1/yColumn Bx2+1xy2+1y
View SolutionColumn Ax=1/yColumn Bx2+x+2x2y2+y+1y
View SolutionColumn Ax<1/y and x and y are positiveColumn B2+x−x2x2y2+y−1y
View SolutionThe graph of the function y = f(x) is as follows.
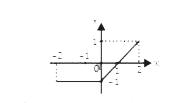
Match the function mentioned in Column-I with the respective graph given in Column-II.
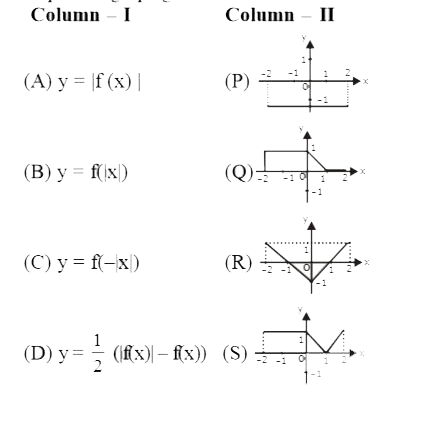
View SolutionLet A={x:−1≤x≤1}=B be a mapping f:A→B . Then, match the following columns: Column I (Function), Column II (Type of mapping) P. f(x)=|x| , a. one-one q. f(x)=x|x| , b. many-one r. f(x)=x3 , c. onto s.f(x)=[x],where[] represents greatest integer function, d. into t. f(x)=sin(πx)2 ,
View SolutionColumn I, Column II y=x2−2x+4x2+2x+4,x∈R,thenycanbe , p. 1 y=x2−3x−22x−3,x∈R,thenycanbe , q. 4 y=2x2−2x+4x2−4x+3,x∈R,thenycanbe , r. −3 x2−(a−3)x+2<0,∀,x∈(−2,3),thanacanbe , s. −10
View SolutionColumn I, Column II Area enclosed , q. 1. sq. units The smaller area included between the curves √x+√|y|=1 and |x|+|y|=1 , r. 4 sq. units Area bounded by the curves y=[x264+2](where[.]de¬es the greatest integer function), y=x−1andx=0 above the x-axis., s. 2/3 sq. units
View SolutionLet L be the line of intersection of the planes 2x+3y+z=1 and x+3y+2z=2 . If L makes an angles α with the positive x-axis, then cosα equals
View SolutionMatch the graph of y = f(x) in Column I with the corresponding graph of y = f'(x) in Column II.


View SolutionLet (x, y) be such that sin−1(ax)+cos−1(y)+cos−1(bxy)=π/2. Match the statements in column I with statements in column II.
Column IColumn IIA) If a = 1 and b = 0, then (x, y)p) lies on the circle x2+y2=1B) If a = 1 and b = 1, then (x, y)q) lies on (x2−1)(y2−1)=0C) If a = 1 and b = 2, then (x, y)r) lies on y = xD) If a = 2 and b = 2, then (x, y)s) lies on (4x2−1)(y2−1)=0
View SolutionLet f(x)=x+1xandg(x)=x+1x+2 Match the composite function given in Column I with respective domains given in Column II Column I, Column II fog(x) , p. R−{−2,−53} gof(x) , q. R−{−1,0} fof(x) , r. R−{0} gog(x) , s. R−{−2,−1} , t R−(−1}
View SolutionFind the range of f(x)=x−[x]1−[x]+x',where[] represents the greatest integer function.
View Solution
