A rectangle with sides of lengths (2n−1)and(2m−1) units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) m2n2 (b) mn(m+1)(n+1) (c) 4m+n−1 (d) non of these Solution in Bengali
Step by step video & image solution for A rectangle with sides of lengths (2n-1) and (2m-1) units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) m^2n^2 (b) mn(m+1)(n+1) (c) 4^(m+n-1) (d) non of these by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Solve loglog2(x2)(x2−10x+22)>0.
View SolutionIf a coin is tossed n times, then find the probability that the head appears odd number of times.
View SolutionThere is a rectangular sheet of dimension (2m−1)×(2n−1), (where m>0,n>0) It has been divided into square of unit area by drawing line perpendicular to the sides. Find the number of rectangles having sides of odd unit length.
View SolutionA rectangle with sides of lengths (2n-1) and (2m-1) units is divided into squares of unit length.The number of rectangles which can be formed with sides of odd length,is (a) m^(2)n^(2) (b) mn(m+1)(n+1) (c) 4^(m+n-1) (d) non of these
View SolutionA rectangle with sides of lengths 15 and 13 unitsis divided into squares of sides of unit length. Thennumber of rectangles which can be formed with thesides of odd length, is
View SolutionIf Sn denotes the sum of first n terms of an A.P. <an> such that SmSn=m2n2, thenaman= a.2m+12n+1 b. 2m−12n−1 c. m−1n−1 d. m+1n+1
View Solutionएक वर्गाकार शीट का आकार (2m−1)×(2n−1) (जहाँ m>0,n>0 ) है इसकी भुजाओं पर लम्ब रेखाएँ खींचकर इसे इकाई क्षेत्रफल के वर्गों में विभाजित किया जाता है । विषम इकाई लम्बाई वाली भजौं के आयतों की संख्या है -
View Solutionएक आयताकार पट्टी की विमा (2m -1) x (2n -1) है, (जहाँ m> 0,n>0). इसे भुजाओं के लम्बवत् रेखायें खींचकर इकाई क्षेत्रफल के वर्गों में विभाजित किया जाता है तब उन आयतों की संख्या, जिनकी भुजायें विषम इकाई लम्बाई की हैं, होगी
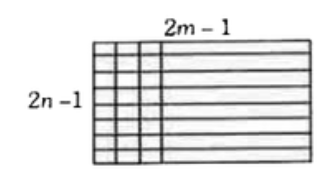
View SolutionA rectangle with sides of lengths (2n−1)and(2m−1) units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) m2n2 (b) mn(m+1)(n+1) (c) 4m+n−1 (d) non of these
View SolutionIf mC1= nC2 then which is correct a. 2m=n b. 2m=n(n+1) c. 2m=(n−1) d. 2n=m(m−1)
View SolutionIf secθ=m,tanθ=n, then 1m[(m+n)+1m+n]....................... A) 2 B) 2m C) 2n D) mn
View SolutionA rectangle with sides of lengths (2n−1)and(2m−1) units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) m2n2 (b) mn(m+1)(n+1) (c) 4m+n−1 (d) non of these
View SolutionA rectangle with sides of lengths (2 n-1) and (2 m-1) units is divided into squares of unit lengths. The number of rectangles which can be formed with sides of odd length is
View Solutionभुजाओं 2m – 1 और 2n – 1 वाले एक आयत को इकाई लंबाई के वर्गों में विभाजित किया गया है। विषम लंबाई की दोनों भुजाओं से बनाये जा सकने वाले आयतों की संख्या है:
View SolutionThere is a rectangular sheet of dimension (2m−1)×(2n−1), (where m>0,n>0) It has been divided into square of unit area by drawing line perpendicular to the sides. Find the number of rectangles having sides of odd unit length.
View SolutionA rectangle with sides 2m-1 and 2n-1 divided into squares of unit length the number of rectangles which can be formed with sides of odd length is
View Solution
