Find the area of the greatest rectangle that can be inscribed in an ellipse x2a2+y2b2=1.Solution in Bengali
Reactangle can be inscribed in the ellipse with its sides parallel ot axes of theellipse as shown in the following figure.
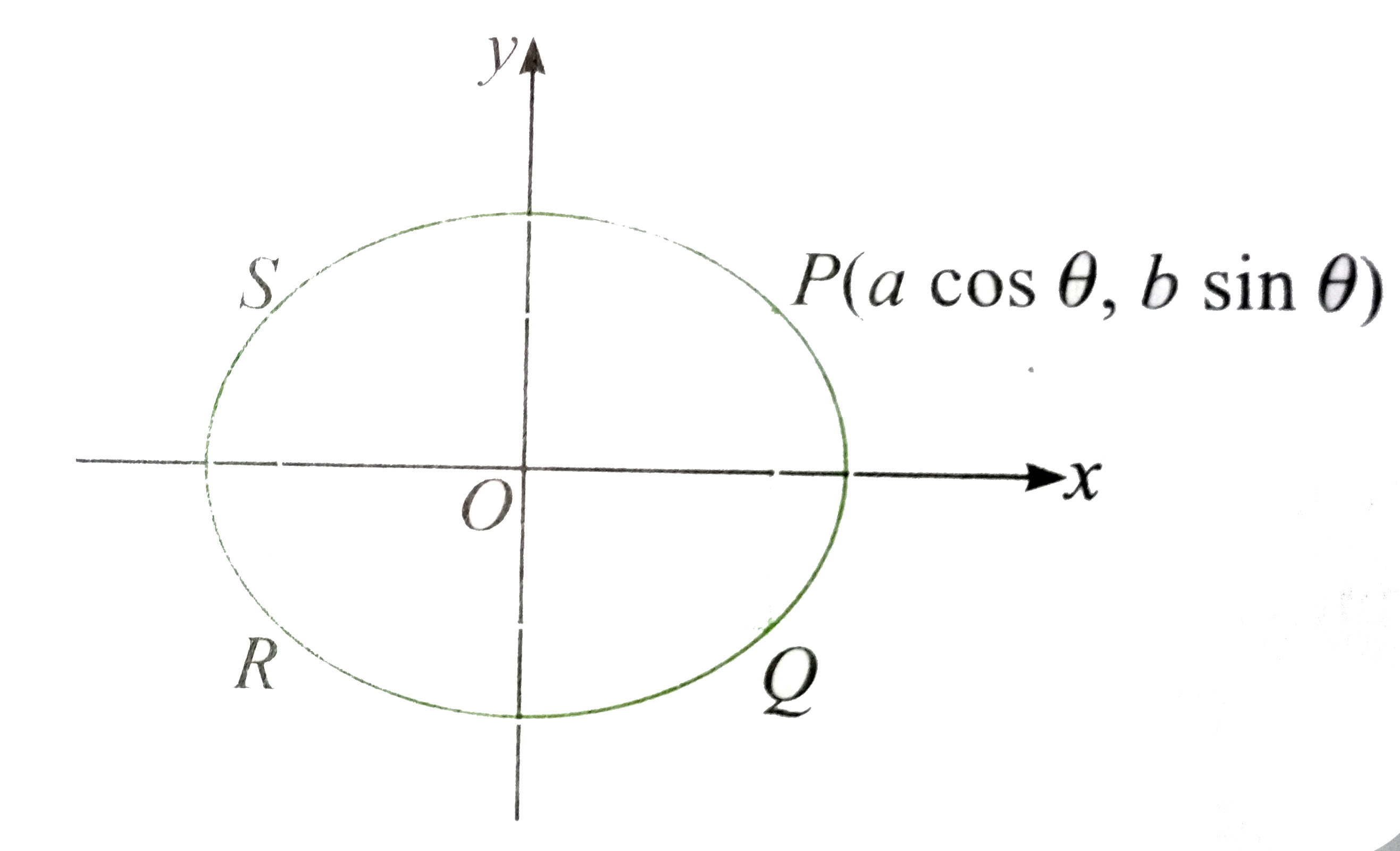
Let P≡(acosθ,bsinθ)
∴ Area o reactangle PQRS
=(2acosθ)(2bsinθ)
=2absin2θ
This is maximum when sin2θ=1
Henece, maximum area =2ab(1)=2ab
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
877 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
The equation esinx−e−sinx−4=0 has
View SolutionLet →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆk and →c=c1ˆi+c2ˆj+c3ˆk be three non- zero vectors such that →c is a unit vectors perpendicular to both the vectors →a and →b. If the angle between →a and →b is π6 then
∣∣ ∣∣a1a2a3b1b2b3c1c2c3∣∣ ∣∣2 is equal to
View SolutionIf the area of the ellipse (x2a2)+(y2b2)=1 is 4π , then find the maximum area of rectangle inscribed in the ellipse.
View SolutionArea of the greatest rectangle inscribed in the ellipse x2a2+y2b2=1 is
View SolutionArea of the largest rectangle that can be inscribed in the ellipse x2a2+y2b2=1 is
View SolutionArea ( in square unit) of the greatest rectangle that can be inscribed in the ellipse x2a2+y2b2=1 is -
View SolutionThe greatest side of the rectangle of the greatest area that can be inscribed in the ellipse x2+2y2=8,is
View Solution2.The area of the greatest rectangle that can be inscribed in the ellipse x29+y2=1is
View SolutionArea of the greatest rectangle inscribed in the ellipse x216+y29=1 is:
View SolutionThe sides of the greatest rectangle that can be inscribed in the ellipse x2a2+y2b2=1 are
View SolutionFind the area of the greatest rectangle that can be inscribed in an ellipse x2a2+y2b2=1
View SolutionFind the area of the greatest rectangle that can be inscribed in an ellipse x2a2+y2b2=1.
View SolutionIf the area of the ellipse (x2a2)+(y2b2)=1 is 4π , then find the maximum area of rectangle inscribed in the ellipse.
View SolutionIf the area of the ellipse (x2a2)+(y2b2)=1 is 4π , then find the maximum area of rectangle inscribed in the ellipse.
View SolutionFind the area of greatest rectangle that can be inscribed in x2a2+y2b2=1.
View SolutionFind the greatest rectangle that can be inscribed in x2a2+y2b2=1
View Solution
