Consider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail then throw a die. Find the conditional probability of the event that the die shows a number greater than 4 given that there is at least one tailSolution in Bengali
According to the equation, sample space
S={(H,H),(H,T),(T,1),(T,2),(T,3),(T,4),(T,5),(T,6)}
In the above set, there are 8 elementary events, but all are not equally likely.
However, events (H,H) and (H,T) are equally likely.
Each event has probability 14 (considering sample space {HH,HT,TH,TT}
Events (T, 1), (T, 2), ...,(T, 6) are also equally likely.
Let probability of each be p. Then
6p=1−14−14=12
∴p=112
Let event A be ''the dice shows a number greater than 4'', and event B be ''there is at least one tail''.
∴A={(T,5),(T,6)}
and B={(H,T),(T,1),(T,2),(T,3),(T,4),(T,5),(T,6)}
∴P(A)=112+112=16
P(B)=14+112+112+112+112+112+112=14+12=34
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Solved Example9videos
PROBABILITY I
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.16videos
PROBABILITY I
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions470videos
PROBABILITY
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE6videos
PROBABILITY II
Similar Questions
When a fair dice is rolled, the number that comes up top is a number between one to six. Assuming we roll the dice once, to check the possibility of three coming up.
03:58View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
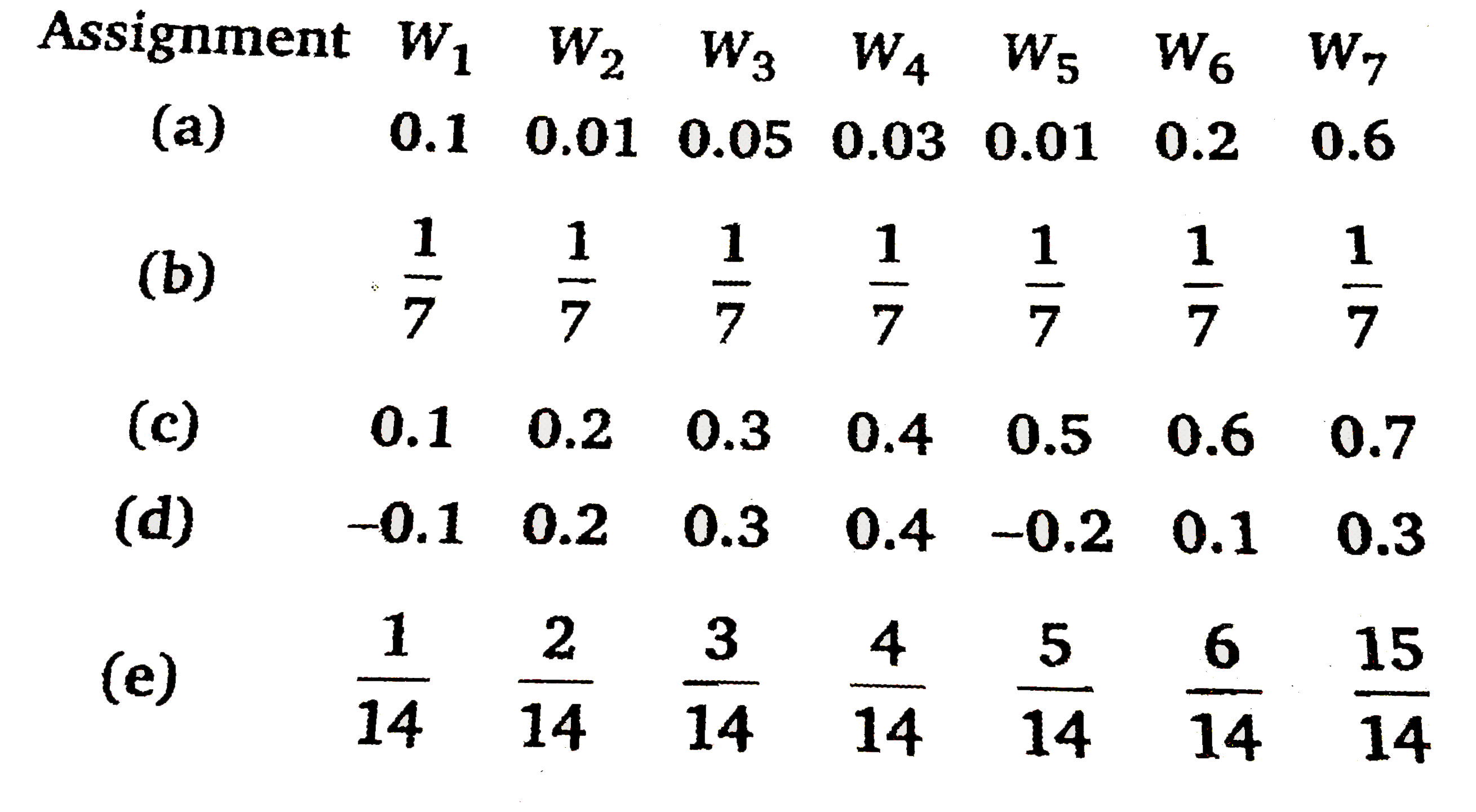 09:02View Solution
09:02View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
04:13View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
03:57View SolutionConsider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail then throw a die. Find the conditional probability of the event that the die shows a number greater than 4 given that there is at least one tail.
10:24View SolutionConsider the experiment of throwing a die, if a multiple of 3 comes up throw the die again and if any other number comes toss a coin. Find the conditional probability of the event the coin shows a tail, given that at least one die shows a 3.
View SolutionConsider a random experiment in which a coin is tossed and if the coin shows head it is tossed again but if it shows a tail then a die is tossed. If 8 possible outcomes are equally likely. Find the probability that the die shows a number greater than 4 if it is known that the first throw of the coin results in a tail.
03:15View Solutionएक सिक्के को उछालने के प्रयोग पर विचार कीजिए | यदि सिक्के पर शीर्ष आता है, तो इसे पुनः उछालिए, परन्तु यदि इस पर पुच्छ है, तो पासा फेंकिए | इस पासा की सप्र्तिबंध प्रायिकता ज्ञात कीजिए कि पसे पर 4 से बड़ी संख्या आती है जबकि दिया है कि कम-से-कम एक पुच्छ आता है |
05:40View SolutionConsider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail, then throw a die. Find the conditional probability of the event that the die shows a number greater than 4 given that there is atleast one tail.
07:14View SolutionConsider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail, then throw a die. Find the conditional probability of the event that the die shows a number greater than 4' given that there is at least one tail.
11:54View SolutionConsider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail, then throw a die. Find the conditional probability of the event that the die shows a number greater than 4' given that there is at least one tail.
04:28View SolutionConsider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail, then throw a die. Find the conditional probability of the event that the die shows a number greater than 4' given that there is at least one tail.
05:40View SolutionConsider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail, then throw a die. Find the conditional probability of the event that the die shows a number greater than 4' given that there is at least one tail.
06:23View SolutionConsider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail then throw a die. Find the conditional probability of the event that the die shows a number greater than 4 given that 'there is at least one tail'.
06:12View SolutionConsider the experiment of throwing a die, if a multiple of 3 comes up throw the die again and if any other number comes toss a coin. Find the conditional probability of the event the coin shows a tail, given that at least one die shows a 2.
10:38View SolutionConsider the experiment of throwing a die. if a multiple of 3 comes tip. throw the die again and if any other number comes, toss a coin Find the conditional probability of the event the coin shows a tail, given that at least one die shows a 3.
09:21View Solution

