If A and B are two events such that P(A) = 12 and P(B) = 23, then show that
(a) P(A∪B)≥23(b)16≤P(A∩B)≤12
(c ) P(A∩¯¯¯B)≤13(d)16≤P(¯¯¯A∩B)≤12Solution in Bengali
P(A)=12andP(B)=23
P(A∪B)≥max {P(A), P(B)} = 23
and P(A∩B)≤min{P(A),P(B)}=12
Now, P(A∩B)=P(A)+P(B)−P(A∪B)≥P(A)+P(B)−1=16
∴16≤P(A∩B)≤12 (1)
P(A∩¯¯¯B)=P(A)−P(A∩B)=12−P(A∩B)
From (1), −12≤−P(A∩B)≤−16
∴0≤12−P(A∩B)≤12−16
∴P(A∩¯¯¯B)≤13
P(¯¯¯A∩B)=P(B)−P(A∩B)=23−P(A∩B)
∴23−12≤23−P(A∩B)≤23−16
16≤P(¯¯¯A∩B)≤12
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Solved Example9videos
PROBABILITY I
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.16videos
PROBABILITY I
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions470videos
PROBABILITY
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE6videos
PROBABILITY II
Similar Questions
When a fair dice is rolled, the number that comes up top is a number between one to six. Assuming we roll the dice once, to check the possibility of three coming up.
08:39View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
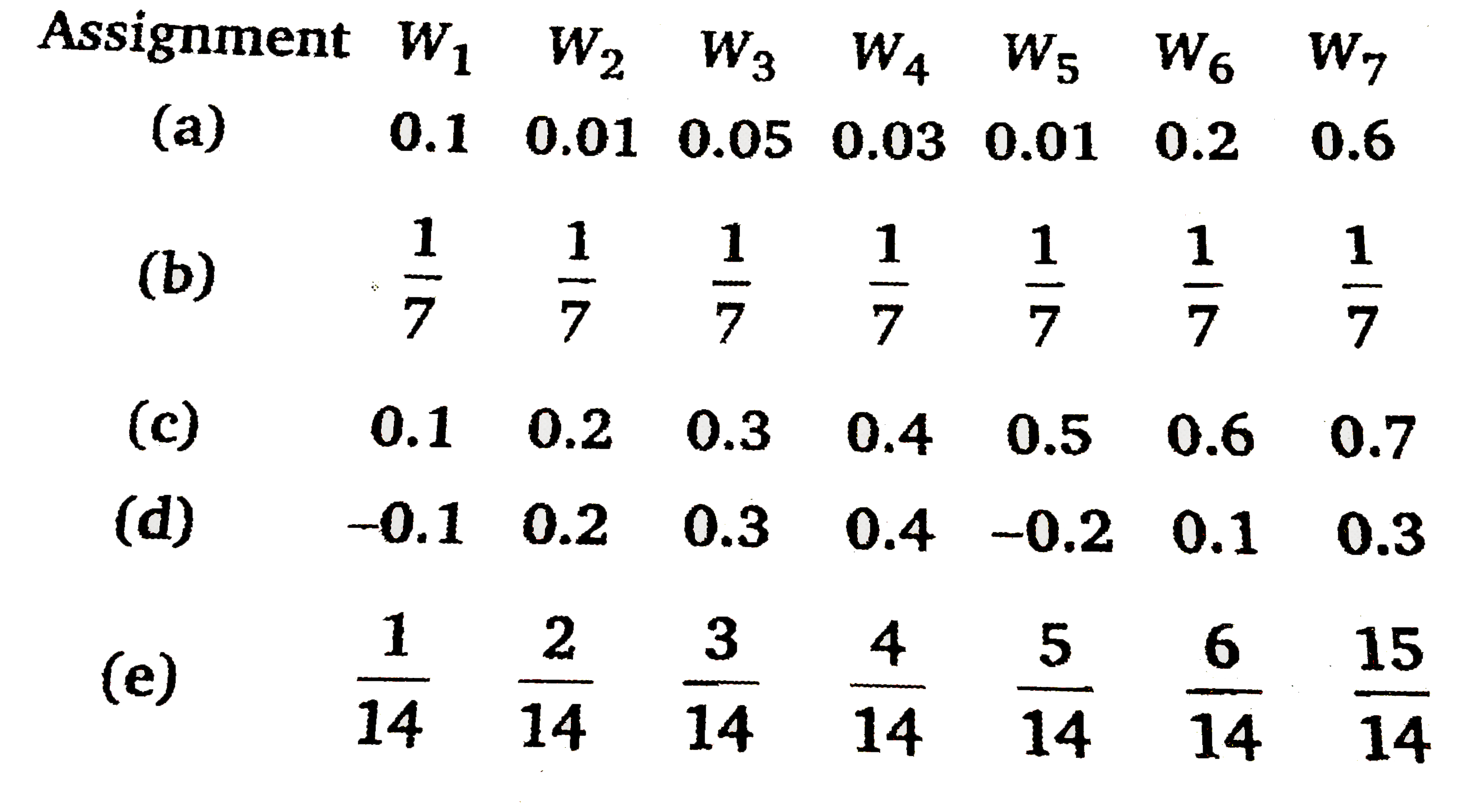 02:17View Solution
02:17View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
02:23View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
04:07View SolutionIf A and B are two events such that P(A) = 12 and P(B) = 23, then show that
(a) P(A∪B)≥23(b)16≤P(A∩B)≤12
(c ) P(A∩¯¯¯B)≤13(d)16≤P(¯¯¯A∩B)≤1203:08View SolutionIf A and B are two events such that P(A∪B)=56,P(A∩B)=13 and P(¯¯¯B)=13 then P(A) =
02:20View SolutionIf two events A and B are such that P(¯¯¯A)=310andP(A∩¯¯¯B)=12, then P(A∩B) is
01:38View SolutionIf A, B are two events such that P(A∪B)≥34and18≤P(A∩B)≤38
03:10View SolutionLet A and B be the two events such that p(A)=12,P(B)=13andP(A∩B)=14 , find
P(¯¯¯A¯¯¯B)03:29View SolutionLet A and B be two events such that P(A∪B)≥3/4and1/8≤P(A∩B)≤3/8
Statement 1 : P(A)+P(B)≥7/8
Statement 2 : P(A)+P(B)≤11/802:26View Solutionयदि A, B दो घटनायें इस प्रकार है कि P(A∪B)≥34 तथा 18≤P(A∩B)≤38 तो
03:51View SolutionIf A and B are two events such that P(A) = 12 and P(B) = 23, then show that
(a) P(A∪B)≥23(b)16≤P(A∩B)≤12
(c ) P(A∩¯¯¯B)≤13(d)16≤P(¯¯¯A∩B)≤1203:21View SolutionIf events A and B are such that P(A)=13,P(B)=12andP(A∩B)=16 , then P (not A and not B) is :
05:54View SolutionIf A and B are two events such that P(A∪B)=56,P(A∩B)=13 and P(¯¯¯B)=13 then P(A) =
06:19View SolutionIf P(A) = 1/2, P(B) = 2/3 then prove that 16≤P(A∩B)≤12
07:19View SolutionIf P(A) = 1/2, P(B) = 2/3, then prove that 16≤P(A∩B)≤12.
06:19View Solution

