A five digit number is formed but the digits 1,2,3,4,5 without repetition. Find the probability that the number is divisible by 4.Solution in Bengali
The correct Answer is:15
Total number of numbers formed by the digits 1, 2, 3, 4, 5 without repetition is 5!=120. Now we know that a number is divisible by 4 if the number placed at its last two digits is divisible by 4. So that last two digits can be 12, 24, 32 or 52, i.e., they can be filled in 4 ways. There are 3!=6 ways of filling the other three places.
Therefore, the favorable numberof ways is 4×6 = 24 ltbgt Hence, the required probability is
P=Favorable no. of casesExhaustive no. of cases=24120=15
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.37videos
PROBABILITY I
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - MCQ54videos
PROBABILITY I
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.16videos
PROBABILITY I
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions470videos
PROBABILITY
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE6videos
PROBABILITY II
Similar Questions
AandB are two candidates seeking admission in IIT. The probability that A is selected is 0.5 and the probability that AandB are selected is at most 0.3. Is it possible that the probability of B getting selected is 0.9?
02:30View SolutionA sample space consists of 3 sample points with associated probabilities given as 2p,p2,4p−1. Then the value of p is p= a.√11−3 b. √10−3 c. 14<p<12 d.none
03:53View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
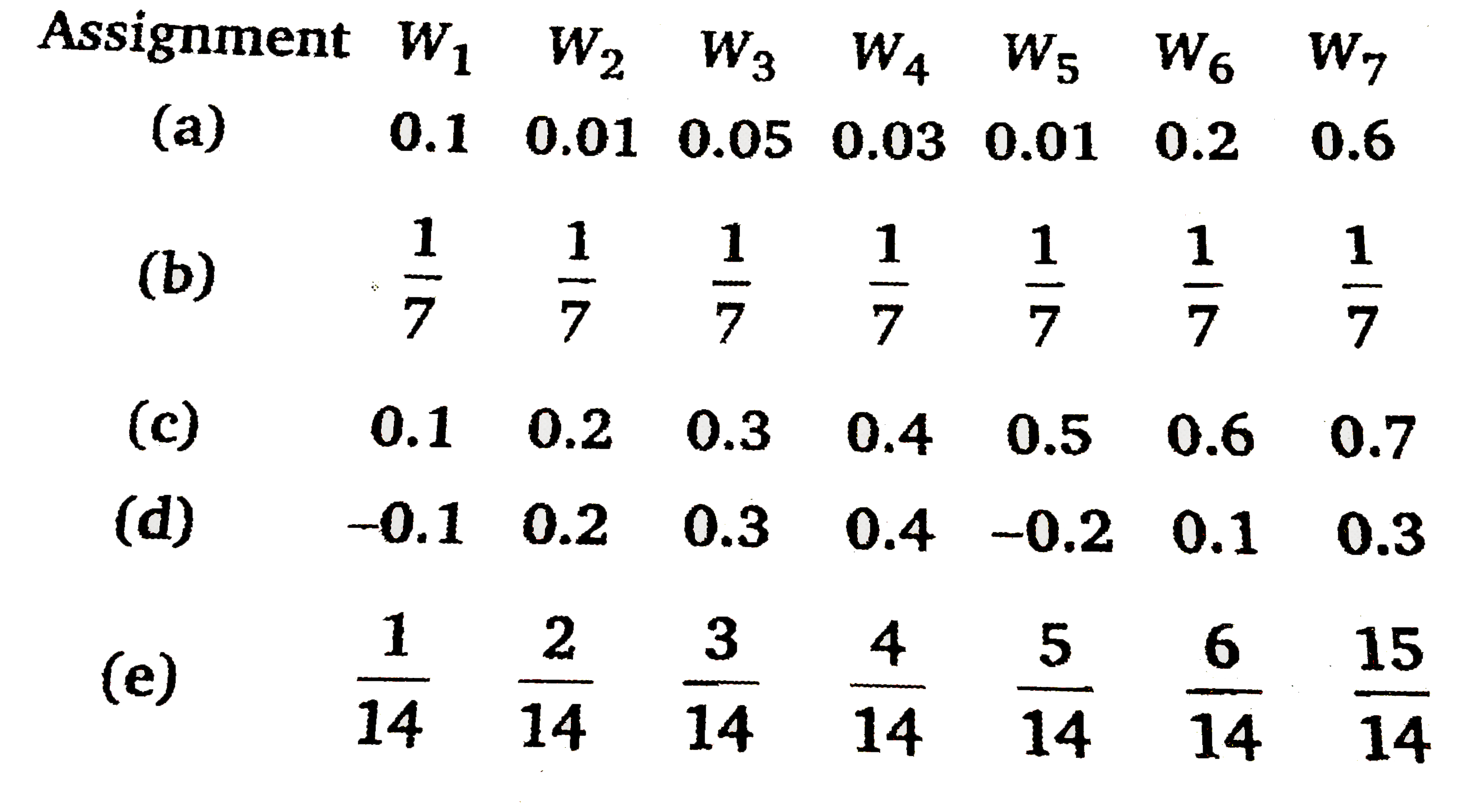 04:21View Solution
04:21View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
02:46View SolutionA five digit number is formed by the digits 1,2,3,4,5 without repetition.
03:55View SolutionA five digit number is formed with the digits 1,2,3,4,5 without repetition. Find the probability that the number is divisible by 4.
06:00View SolutionA five-digit number is formed by the digit 1, 2, 3, 4, 5 without repetition. Find the probability that the number formed is divisible by 4.
04:04View SolutionA five digit number is formed with the digits 0,1,2,3and 4 without repetition ,Find the chance that the number is divisible by 5.
03:52View SolutionA five digit number is formed by the digit 1,2,3,4 and 5 without repetition. Find the probability that the number formed is divisible by 4.
01:39View SolutionA five digit number is formed by the digits 1,2,3,4,5 with no digit being repeated. The probability that the number is divisible by 4, is
04:54View SolutionA 4 digit number made of digits 1,2,3,4,5 is wirtten down at random without repetition. The probability that the number so formed is divisible by 6 is
03:44View SolutionA five digit number is formed with the digits 1,2,3,4,5 without repetition. Find the probability that the number is divisible by 4.
04:03View SolutionA five-digit number is formed by the digit 1, 2, 3, 4, 5 without repetition. Find the probability that the number formed is divisible by 4.
01:27View SolutionA five digit number is formed with the digits 1,2,3,4,5 without repetition. Find the probability that the number is divisible by 4.
02:56View SolutionA five digit number is formed by the digits 1, 2, 3, 4, 5 without repetition. Find the probability that the number is divisible by 4.
04:45View Solution

