Show that [(p→q)∧(q→r)]→(p→r)is a tautology Solution in Bengali
Truth values of [(p→q)∧(q→r)]→(p→r)
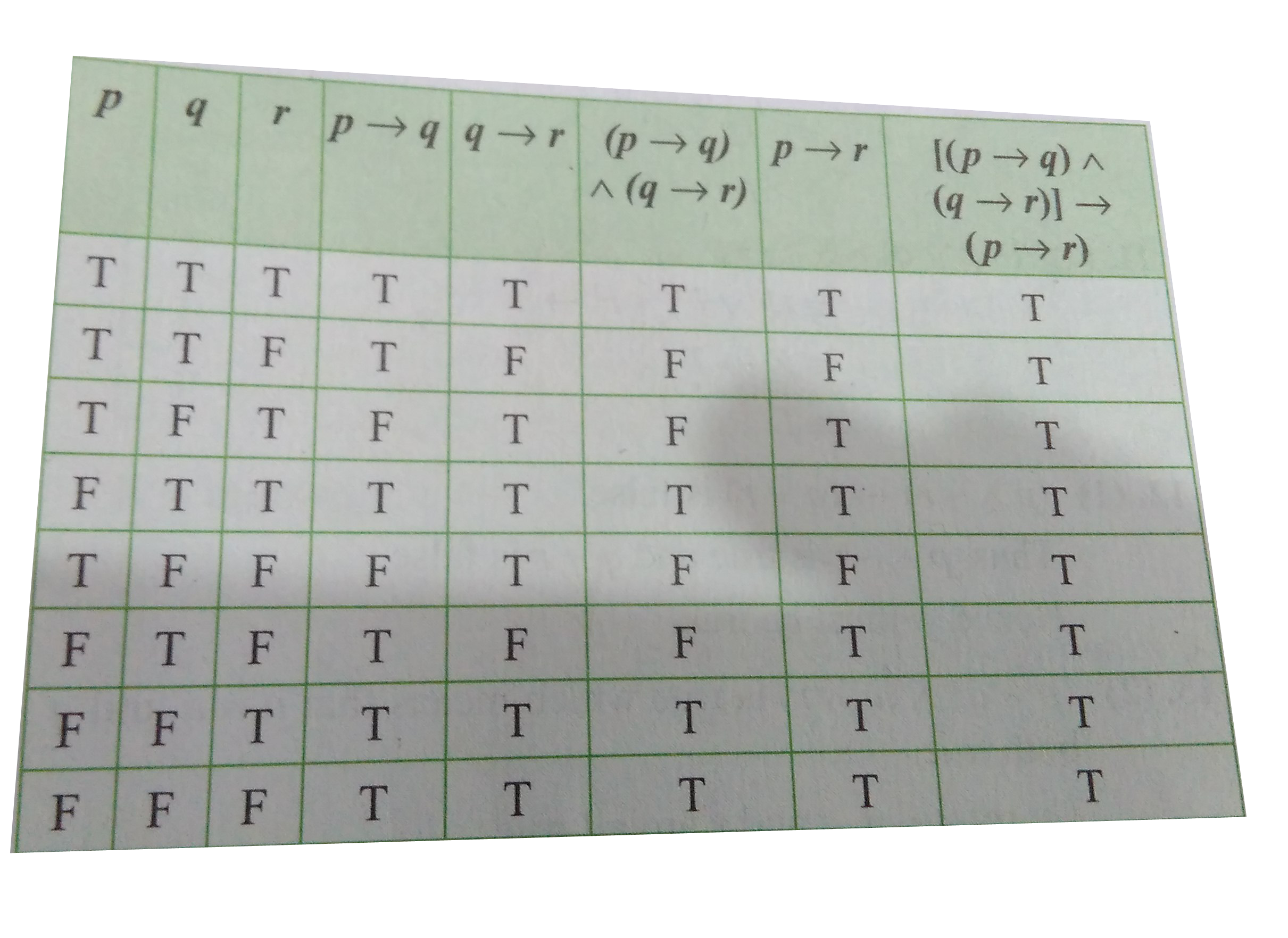
For all possible truth values of p and q , the compound statement [(p→q)∧(q→r)]→(p→r) is true.
Thus, [(p→q)∧(q→r)]→(p→r) is a tautolgy.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - MATHMETICAL REASONINGEXERCISE - Single correct answer type38videos
MATHMETICAL REASONING
- BOOK - CENGAGE PUBLICATIONCHAPTER - MATHMETICAL REASONINGEXERCISE - Archives10videos
MATHMETICAL REASONING
- BOOK - CENGAGE PUBLICATIONCHAPTER - MATHMETICAL REASONINGEXERCISE - Archives10videos
MATHMETICAL REASONING
- BOOK - CENGAGE PUBLICATIONCHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - JEE ADVANCED1videos
LOGARITHM AND ITS PROPERTIES
- BOOK - CENGAGE PUBLICATIONCHAPTER - MATRICESEXERCISE - All Questions509videos
MATRICES
Similar Questions
Which of the following is not a statement.
04:26View SolutionStatements -1 : ~(p↔~q) is equivalent to p↔q
Statement-2: ~(p↔~q) is a tautology.05:52View SolutionStatements -1 : ~(p↔~q) is equivalent to p↔q
Statement-2: ~(p↔~q) is a tautology.03:04View SolutionLet (x0,y0) be the solution of the following equations: (2x)1n2=(3y)1n3 31nx=21ny The x0 is 16 (b) 13 (c) 12 (d) 6
06:38View SolutionIn which of the following type of matrix inverse does not exist always? a. idempotent b. orthogonal c. involuntary d. none of these
01:32View SolutionShow that [(p→q)∧(q→r)]→(p→r)is a tautology
04:56View SolutionConsider :
Statement I:
(p∧~q)∧(~p∧q) is a fallacy
Statement II: (p→q)↔(~q→~p) is a tautology06:21View SolutionAssuming p and q as given, write the verbal statement for the following symoblic statements :
p : It is a day time. " " q : It is warm.
(i) p∧~q (ii) ~p→q (iii) q→p01:48View SolutionPrepare truth tables for the following statements :
(1) p→(q→p)
(2) [(p→q)∧q]→p
(3) (p→q)⇔(~p∨q)
(4) (q→p)∨(~p⇔q)
(5) (p⇔r)∧(q⇔p).01:53View SolutionShow that p∨(~p) is a tautology.
01:18View SolutionLet p,q,r be the statements p: X is a rectangle, q: x is a square, r:p→q Show that p→r is not a tautology.
02:53View SolutionVerify whether the following compound propositions are tautologies or contradictions or contingency
((p→q)∨(q→r))→(p→r)07:45View SolutionShow that (p∧q)→(p∨q) is a tautology.
02:41View SolutionShow that [¬p∨¬q]∨p is a tautology.
04:05View SolutionEach of the statement p→q,q→rand~r is true. Then
04:57View SolutionShow that [(p→q)∧(q→r)]→(p→r)is a tautology
04:47View Solution

