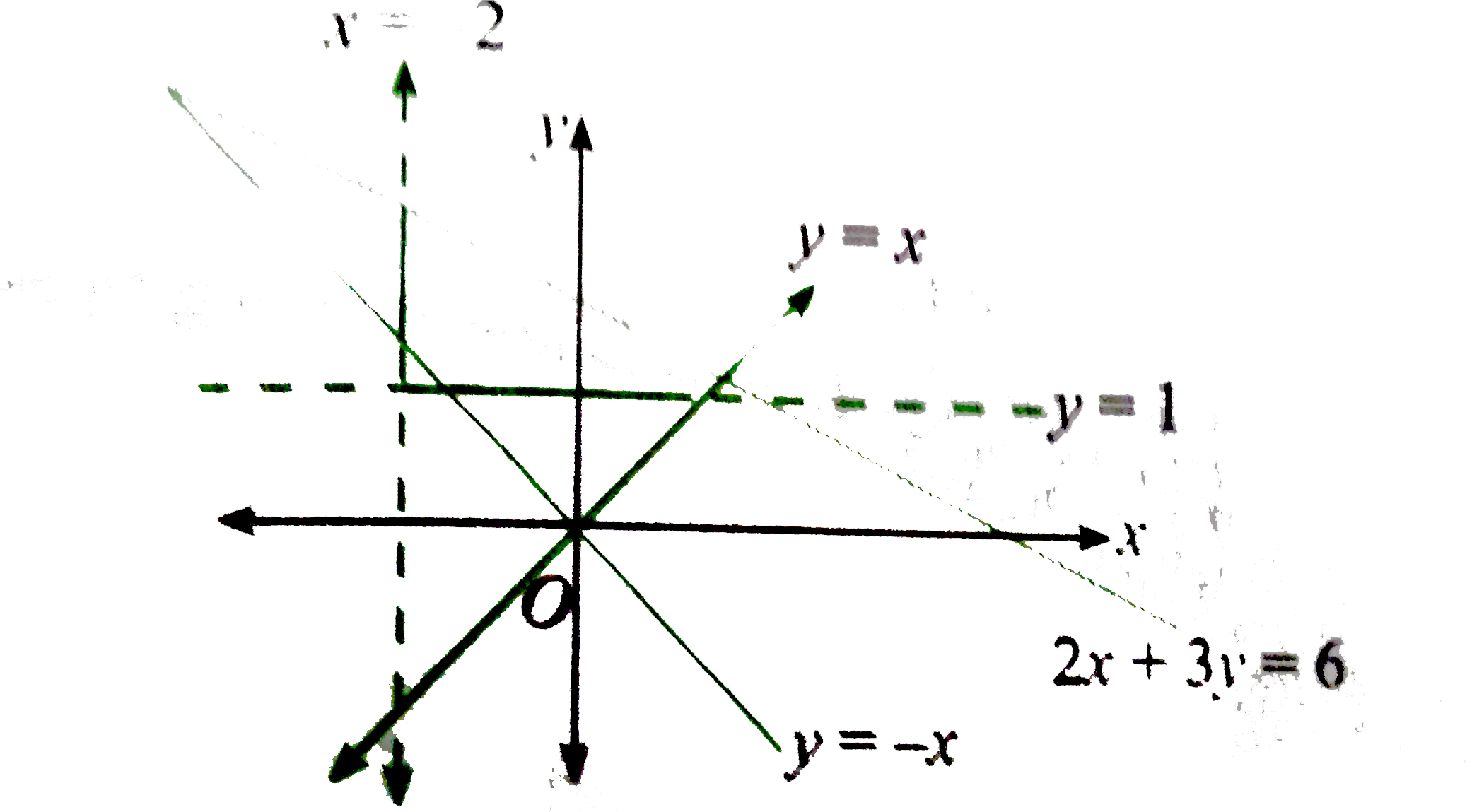
The combined equation of three sides of a triangle is (x2−y2)(2x+3y−6)=0 if (-2,a) is an interior point and (b,1) is an exterior point of the triangle, thenSolution in Bengali
2<a<10/3
−2<a<10/3
−1<b<9/2
−1<b<1
The correct Answer is:1,4
The separate equations of the sides are x−y=0,x+y=0and2x+3y−6=0 . The point (-2,a) moves on the line x=−2 and the point (b,1) moves on the line y=1 . From the figure , the y- coordinates of the points of intersection of x=−2 with y=−xand2x+3y=6 given the range of values of a . The x - coordinates of the points of intersection of y=1 with y=−xandy=x give the range of values of b.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Linked Comprehension Type6videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Single Correct Answer type23videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Matching Column Type1videos
PARABOLA
Similar Questions
If λx2−10xy+12y2+5x−16y−3=0, represents a pair of straight lines, then the value of λ is
04:22View SolutionThe distance between the lines (x+7y)2+4√2(x+7y)−42=0 is_____________
05:00View SolutionThe angle between the pair of lines whose equation is 4x2+10xy+my2+5x+10y=0, is
02:15View SolutionLet f:R→R,y=f(x),f(0)=0,f'(x)>0andf''(x)>0. Three point A(α,f(α)),B(β,f(β)),C(γ,f(γ))ony=f(x) such that 0<α<β<γ.
Which of the following is false ?04:18View SolutionAB is a chord of y2=4x such that normals at A and B intersect at C(9,6) and the tengent at A and B at point T, find (CT)2/13
02:40View SolutionThe three sides of a triangle are given by (x^(2)-y^(2))(2x+3y-6)=0. If the points (-2, a) lies inside and (b,1) lies outside the triangle,then
05:02View SolutionThe combined equation of three sides of a triangle is (x2−y2)(2x+3y−6)=0 . If (−2,a) is an interior point and (b,1) is an exterior point of the triangle, then 2<a<103 (b) −2<a<103 −1<b<92 (d) −1<b<1
05:02View SolutionThe point (-2,a) lies in the interior of the triangle formed by the lines y=x,y=-x and 2x+3y=6 the integral value of a is
View SolutionThe combined equation of three sides of a triangle is (x^(2)-y^(2))(2x+3y-6)=0. If (sec theta,1) is an interior point of the triangle then find the value of theta
06:15View SolutionIf the lines x+y=0,x-y=0 and 2x+3y=6=0 are the sides of a triangle and (-2,a) is an interior point of the triangle then a lies
08:41View SolutionThe combined equation of three sides of a triangle is (x2−y2)(2x+3y−6)=0. If (-2, a) is an interior point of the triangle, then
03:32View SolutionThe combined equation of three sides of a triangle is (x2−y2)(2x+3y−6)=0. If (-2, a) is an interior point of the triangle, then
05:31View SolutionThe combined equation of the three sides of a triangle is (x2−y2)(2x+3y−6)=0. If the point (0,α) lies in the interior of this triange then
05:43View SolutionThe sides of a triangle are 3x+2y−6=0,2x−3y+6=0,x+2y+2=0. P(0,b) is a point on y-axis. If P lies on the triangle or inside the triangle then the range of b is
05:02View SolutionThe combined equation of three sides of a triangle is (x2−y2)(2x+3y−6)=0 . If (−2,a) is an interior point and (b,1) is an exterior point of the triangle, then 2<a<103 (b) −2<a<103 −1<b<92 (d) −1<b<1
04:14View SolutionThe combined equation of three sides of a triangle is (x2−y2)(2x+3y−6)=0 . If (−2,a) is an interior point and (b,1) is an exterior point of the triangle, then
08:42View Solution

