Solve $cos 2 x > | sin x |, x \in (- \frac{π}{2}, π)$ Solution in Bengali

Video Solution

Text Solution

Verified by Experts

Draw the graphs of $y = cos 2 x and y = | sin x |$ .

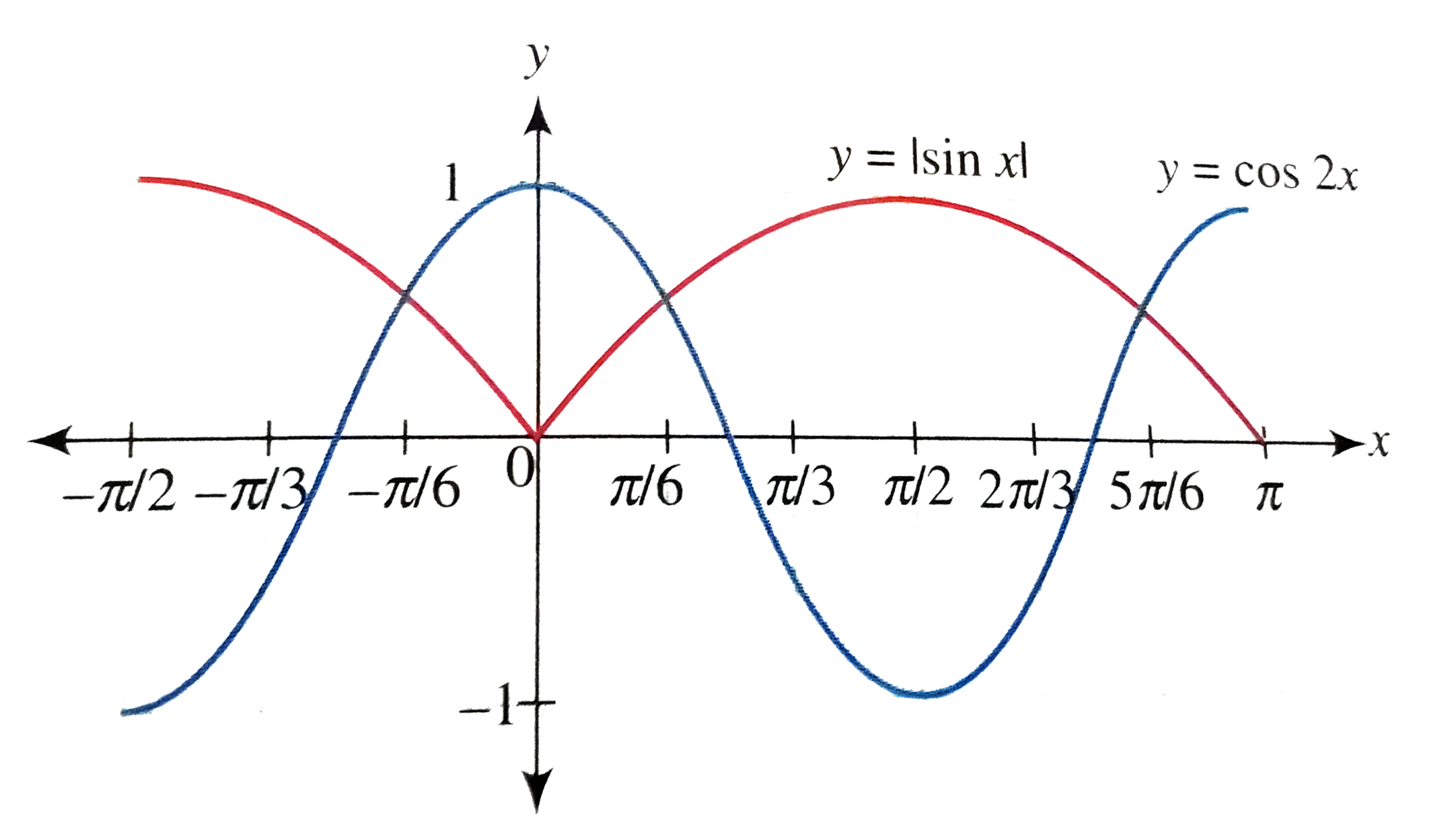
Let $cos 2 x = sin x$
$\Rightarrow 2 {sin}^{2} x + sin x - 1 = 0$
$\Rightarrow sin x = - 1, \frac{1}{2}$
But $sin x \neq - 1 \Rightarrow sin x = \frac{1}{2}$ Clearly, from the graphs of $y = | sin x | and y = cos 2 x, x = \pm \frac{π}{6}, \frac{5 π}{6}$ .
For $cos 2 x > | sin x |$ , the graph of $y = cos 2 x$ must lie abvoe the graph of $y = | sin x |$ .
From the graph the solution set is $x \in (- \frac{π}{6}, \frac{π}{6}) \cup (\frac{5 π}{6}, π)$ .

|

Updated on:21/07/2023

Class 12 MATHS LINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-GRAPHICAL TRANSFORMATIONS-ILLUSTRATION

Home
Ask Doubt
Profile