Question

Find the equation of the projection of the line ${\displaystyle \frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-3}{4}}$ on the plane ${\displaystyle x+2y+z=9}$.

Explanation

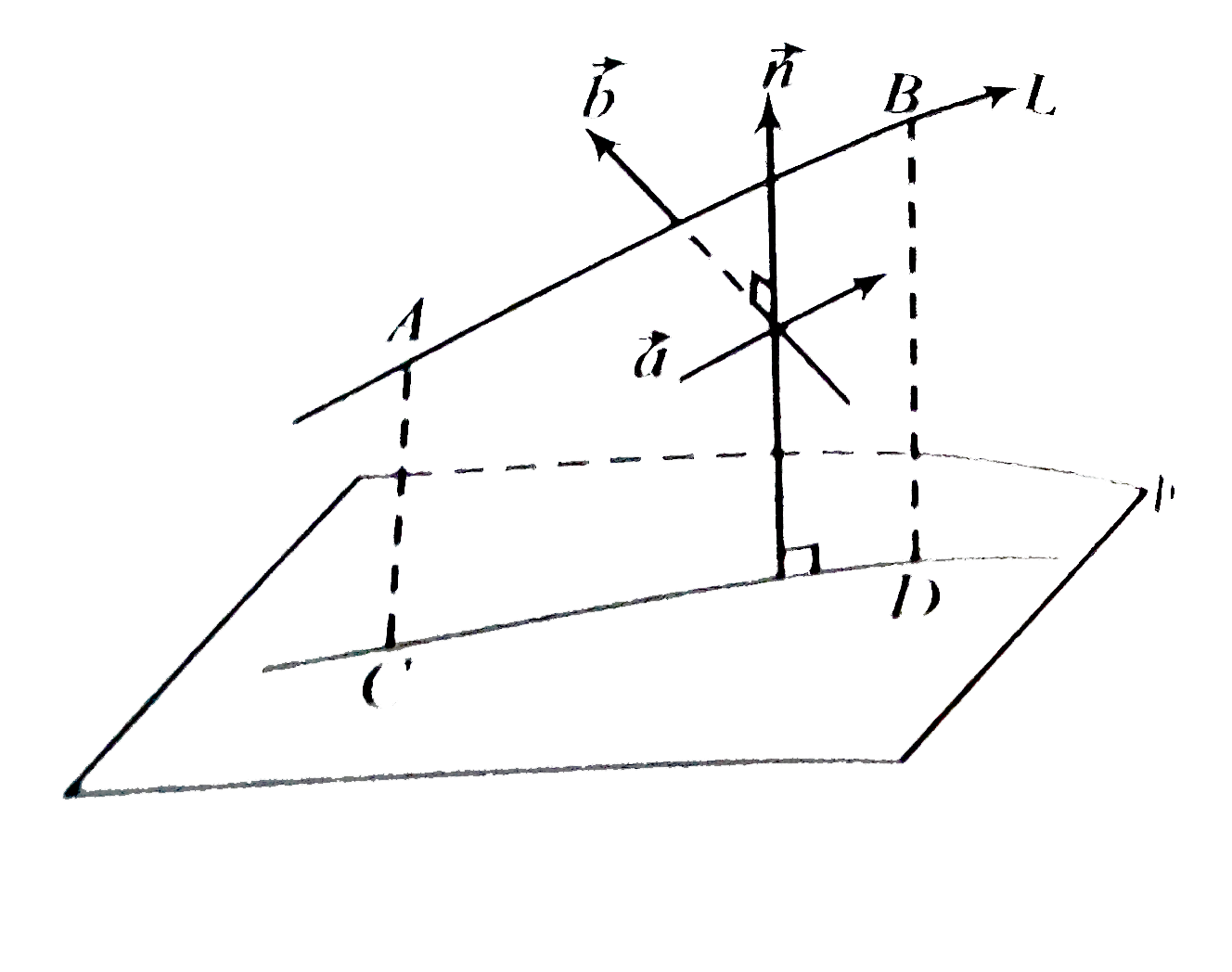
Projection of given line `L-=(x-1)/(2)= (y+1)/(-1)=(z-3)/(4)` on given plane `P-=x+2y+z=9` is the line of intersection of plane P and plane (ABCD) through the line L and perpendicular to the plane P.
Now line L is parallel to vector `veca=2hati-hatj+4hatk`.
Vector normal to plane `P` is `vecn=hati+2hatj+hatk" "`(ii)
`therefore` Vector normal plane ABCD is `vecb=vecaxxvecn= |{:(hati,,hatj,,hatk),(2,, -1,,4),(1,,2,,1):}|=-9hati+2hatj+5hatk`
Plane ABCD passes through the line L, i.e., passes through the point (1, -1, 3). Thus,
`" "` Equation of plane `ABCD = (-9)(x-1)+2(y+1)+5(z-3)=0 or 9x-2y-5z+4=0" "`(iii)
Now required projection is line of intersection of given plane P and plane ABCD
or `" "x+2y+z-9=9x-2y-5z+4`