A parallelepiped is formed by planes drawn through the points P(6,8,10)and(3,4,8) parallel to the coordinate planes. Find the length of edges and diagonal of the parallelepiped.Solution in Bengali
From the figure, it is clear that the length of the edges of the parallelepiped a,b,c is x2−x1,y2−y1,z2−z1 or 6−3,8−4and10−8or3,4and2. Therefore,
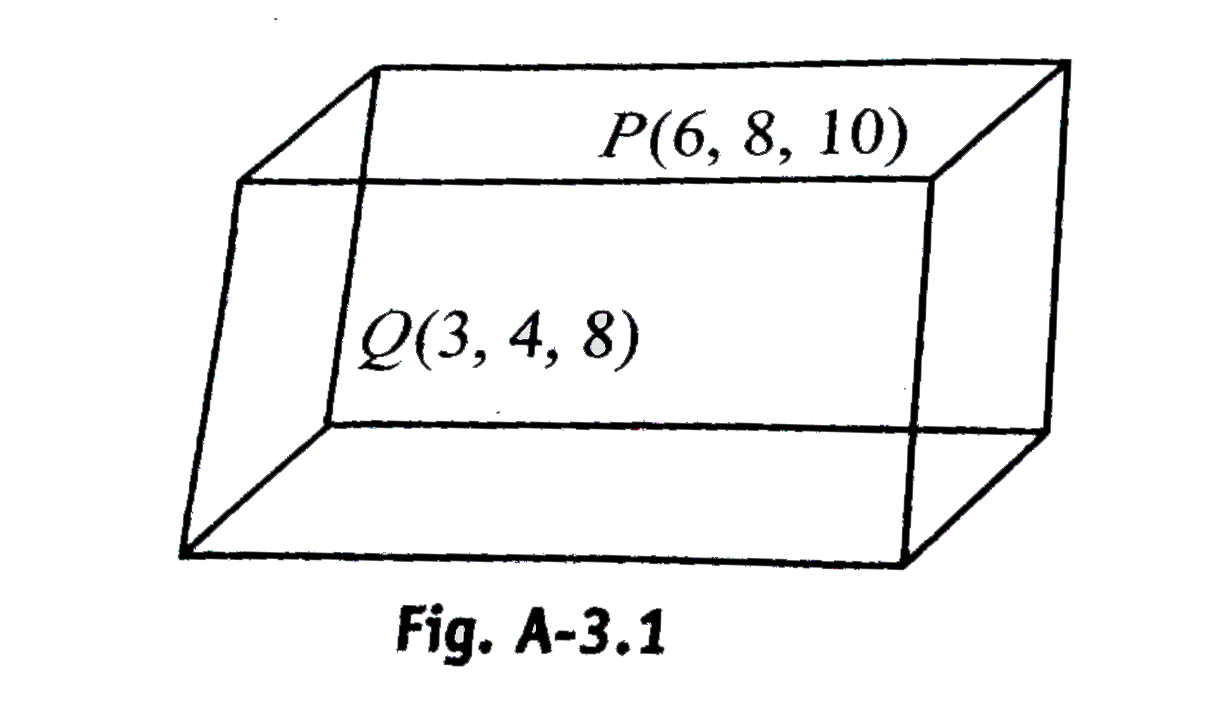
The length of the diagonal will be
√a2+b2+c2=√9+16+4=√39.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - CONCEPT APPLICATION EXERCISE 3.215videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - CONCEPT APPLICATION EXERCISE 3.319videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES INTEGER TYPE1videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
Similar Questions
Find the point where line which passes through point (1,2,3) and is paralle to line →r=ˆi+ˆj+2ˆk+λ(ˆi−2ˆj+3ˆk) meets the xy-plane.
05:19View SolutionFind the angle between the line x−13=y−12=z−14 and the plane 2x+y−3z+4=0.
01:10View SolutionIf the distance between the plane ax 2y + z = d and the plane containing the lines x−12=y−23=z−34 and x−23=y−34=z−45 is √6 , then value of |d| is
01:10View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
02:59View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
02:59View SolutionA parallelepiped is formed by planes drawn through the points P(6,8,10)and(3,4,8) parallel to the coordinate planes. Find the length of edges and diagonal of the parallelepiped.
03:20View SolutionA parallelepiped is formed by planes drawn through the points (2,3,5)and(5,9,7) , parallel to the coordinate planes. The length of a diagonal of the parallelepiped is a.7 unit b. √38 unit c. √155 unit d. none of these
02:41View SolutionA parallelepiped is formed by planes drawn through the points P(6,8,10) and Q(3,4,8) parallel to the coordinate planes.Find the length of edges and diagonal of the parallolepiped.
02:18View SolutionPlanes r drawn parallel to the coordinate planes through the point P(x1,y1, z1) and Q(x2,y2,z2) . Find the length of the edges of the parallelepiped so formed.
01:11View SolutionPlanes are drawn parallel to the coordinate planes through the points (3,0,-1) and (-2,5,4). Find the lengths of the edges of he parallelepiped so formed.
00:58View SolutionIf a parallelepiped is formed by the planes drawn through the points (2,3,50 and (5,9,7) parallel to the coordinate planes, then write the lengths of edges of the parallelopiped and length of the diagonal.
01:41View SolutionFind the lengths of the edges of the rectangular parallelepiped formed by planes drawn throgh points (1,2,3) and (4,7,6) parallel to the co ordinate planes
01:51View SolutionA parallelepiped is formed by planes drawn through the points P(6,8,10)and(3,4,8) parallel to the coordinate planes. Find the length of edges and diagonal of the parallelepiped.
04:34View SolutionA parallelepiped is formed by planes drawn through the points P(6,8,10)and(3,4,8) parallel to the coordinate planes. Find the length of edges and diagonal of the parallelepiped.
01:53View SolutionA parallelepiped is formed by planes drawn parallel to coordinate axes through the points A=(1,2,3) and B=(9,8,5). The volume of that parallelepiped is equal to (in cubic units)
01:28View SolutionPlanes are drawn parallel to the coordinate planes through the points (3,0,-1) and (-2,5,4). Find the lengths of the edges of he parallelepiped so formed.
02:38View Solution

