The coordinates of the foot of the perpendicular drawn from the origin to the line joining the point (−9,4,5)and(10,0,−1) will be a. (−3,2,1) b. (1,2,2) c. (4,5,3) d. none of theseSolution in Bengali
(-3,2,1)
(1,2,2,)
(4,5,3)
none of these
The correct Answer is:D
Let AD be the perpendicular and D be the foot of the perpendicular which divides BC in the ratio λ:1, then
D(10λ−9λ+1,4λ+1,−λ+5λ+1) (i)
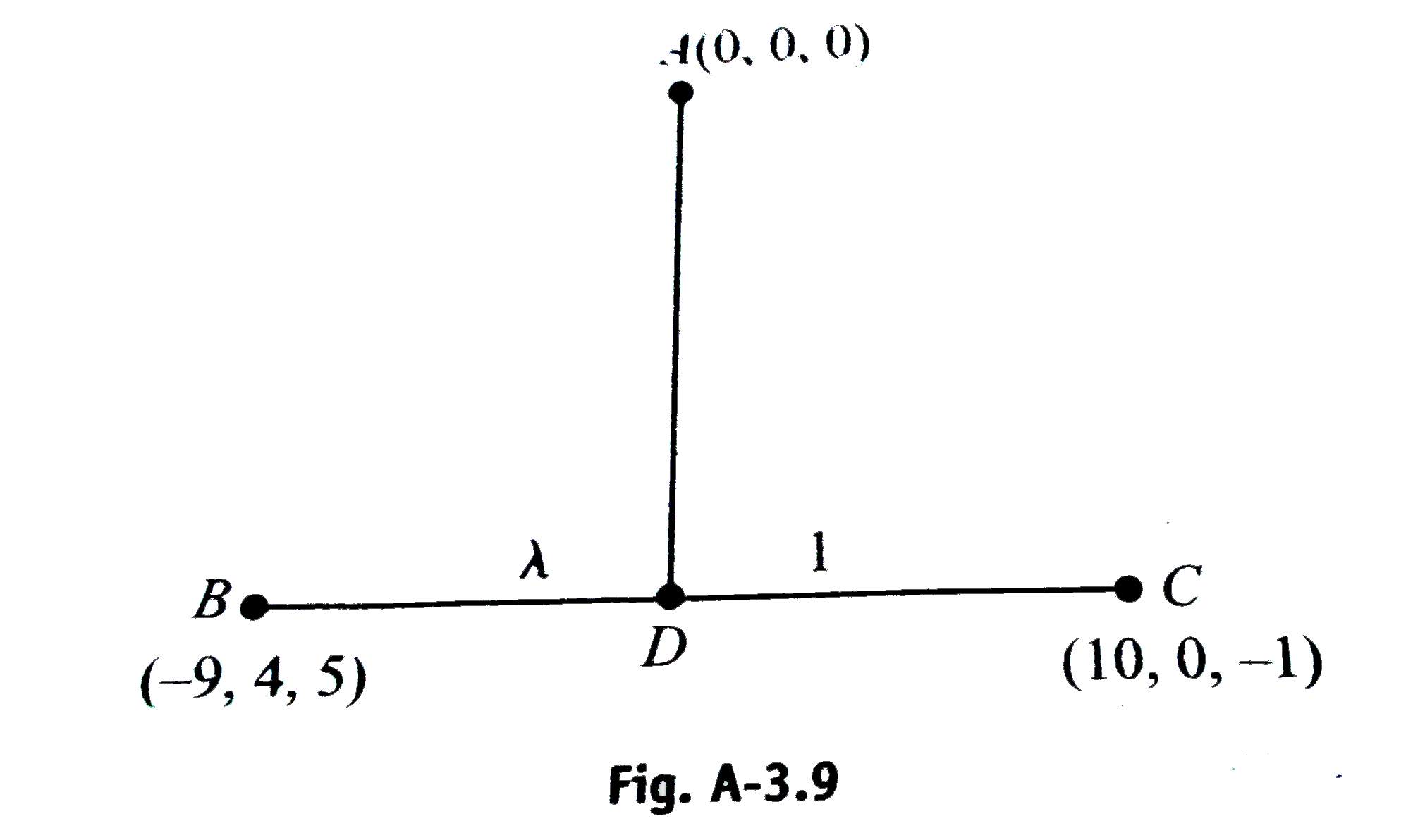
The direction ratio of AD are 10λ−0λ+1,4λ+1and−λ+5λ+1 and direction ratios of BC are 19,-4 and -6.
Since AD⊥BC, we get
19(10λ−9λ+1)−4(4λ+1)−6(−λ+5λ+1)=0
or λ=3128
Hence, on putting the value of λ in (i) ,we get required foot of the perpendicular, i.e., (5859,11259,10959).
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CORRECT ANSWER TYPE17videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - REASONING TYPE10videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - SUBJECTIVE TYPE17videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
Similar Questions
Let PM be the perpendicular from the point P(1,2,3) to the x−y plane. If →OP makes an angle θ with the positive direction of the z− axis and→OM makes an angle φ with the positive direction of x− axis, whereO is the origin and θandφ are acute angels, then a. cosθcosφ=1/√14 b. sinθsinφ=2/√14 c. tanφ=2 d. tanθ=√5/3
06:08View SolutionStatement 1: Lines →r=ˆi+ˆj−ˆk+λ(3ˆi−ˆj)and→r=4ˆi−ˆk+μ(2ˆi+3ˆk) intersect. Statement 2: →b×→d=0 , then lines →r=→a+λ→band→r=→c+λ→d do not intersect.
06:05View SolutionIf the direction cosines of a variable line in two adjacent points be l,m,nandl+δl,m+δm,n+δn the small angle δθas between the two positions is given by
05:42View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
15:02View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
03:36View SolutionFind the coordinates of the foot of the perpendicular drawn from the point A(1,2,1) to the line joining B(1,4,6)andC(5,4,4).
06:52View SolutionFind the coordinates of the foot of perpendicular drawn from th point A(1,8,4) to the line joining the points B(0,−1,3)and C(2−3,−1).
06:05View SolutionThe coordinates o the foot of the perpendicular drawn from the origin to the line joining the point (−9,4,5)and(10,0,−1) will be a. (−3,2,1) b. (1,2,2) c. 4,5,3 d. none of these
05:16View SolutionFind the coordinates of the foot of the perpendicular drawn from the point A(1,8,4) to the line joining the points B(0,-1,3) and C(2,-3,-1)
05:11View SolutionThe point in which the join of (-9,4,5) and (11,0,-1) is met by the perpendicular from the origin is-
04:15View Solutionबिंदुओं (-9,4,5) व (10,0,-1) को मिलाने वाली रेखा पर मूलबिंदु से डाले गए लम्ब के पाद बिंदु के निर्देशांक हैं
03:48View SolutionFind the coordinates of the foot of perpendicular drawn from th point A(1,8,4) to the line joining the points B(0,−1,3)andC(2−3,−1).
05:42View SolutionFind the coordinates of the foot of the perpendicular drawn from point A(1,0,3) to the join of points B(4,7,1)andC(3,5,3).
08:51View SolutionThe coordinates o the foot of the perpendicular drawn from the origin to the line joining the point (−9,4,5)and(10,0,−1) will be a. (−3,2,1) b. (1,2,2) c. 4,5,3 d. none of these
05:36View SolutionFind the coordinates of the foot of the perpendicular drawn from point A(1,0,3) to the join of points B(4,7,1)andC(3,5,3).
View SolutionThe coordinates of the foot of the perpendicular drawn from the origin to the line joining the point (−9,4,5) and (10,0,−1) will be
04:37View Solution

