The lines which intersect the skew lines y=mx,z=c;y=−mx,z=−c and the x-axis lie on the surface a. cz=mxy b. xy=cmz c. cy=mxz d. none of theseSolution in Bengali
cz=mxy
xy=cmz
cy=mxz
none of these
The correct Answer is:c
Equations of the planes through y=mx,z=candy=−mx,z=−c are respectively,
(y−mx)+λ1(z−c)=0 (i)
and (y+mx)+λ2(z+c)=0 (ii)
It meets at x-axis, i.e., y=0=z.
∵λ2=λ1
From (i) and (ii), y−mxz−c=y+mxz+c
∵cy=mzx
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CORRECT ANSWER TYPE
17 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - REASONING TYPE
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - SUBJECTIVE TYPE
17 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
291 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)
4 Videos
Similar Questions
Let PM be the perpendicular from the point P(1,2,3) to the x−y plane. If →OP makes an angle θ with the positive direction of the z− axis and→OM makes an angle φ with the positive direction of x− axis, whereO is the origin and θandφ are acute angels, then a. cosθcosφ=1/√14 b. sinθsinφ=2/√14 c. tanφ=2 d. tanθ=√5/3
View SolutionStatement 1: Lines →r=ˆi+ˆj−ˆk+λ(3ˆi−ˆj)and→r=4ˆi−ˆk+μ(2ˆi+3ˆk) intersect. Statement 2: →b×→d=0 , then lines →r=→a+λ→band→r=→c+λ→d do not intersect.
View SolutionIf the direction cosines of a variable line in two adjacent points be l,m,nandl+δl,m+δm,n+δn the small angle δθas between the two positions is given by
View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
View SolutionIf x+y+z=0 prove that |axbyczcyazbxbzcxay|=xyz|abaca|
View SolutionProve that |(b+x)(c+x)(v+x)(a+x)(a+x)(b+x)(b+y)(c+y)(c+x)(a+t)(a+y)(b+y)(b+z)(c+z)(c+z)(a+z)(a+z)(b+z)|=(b−c)(c−a)(y−z)(x−y).
View SolutionIf A =[(a,b,c),(x,y,z),(l,m,n)] is a skew-symmetric matrix,m nthen which of the following is equal to x+ y+ z?
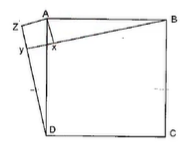
View SolutionIn Figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY=3 cm and AZ=2 cm, then BY=
(a) 5cm
(b) 6cm
(c) 7cm
(d) 8cm
View SolutionIf x=a+m, y=b+m, z=c+m , the value of x2+y2+z2−yz−zx−xya2+b2+c2−ab−bc−ca is (a) 1 (b) x+y+za+b+c (c) a+b+cx+y+z (d) not possible to find
View Solutionयदि ∣∣ ∣ ∣∣a−bb−cc−ax−yy−zz−xp−qq−rr−p∣∣ ∣ ∣∣=m∣∣ ∣ ∣∣cabzxyrpq∣∣ ∣ ∣∣ तो m का मान है-
View SolutionIf xb+c=yc+a=za+b, then show that ay+z−x=bz+x−y=cx+y−z .
View Solutionযদি xb+c=yc+a=za+b হয়, দেখাই যে, ay+z−x=bz+x−y=cx+y−z
View SolutionThe lines which intersect the skew lines y=mx,z=c;y=−mx,z=−c and the x-axis lie on the surface: (a.) cz=mxy (b.) xy=cmz (c.) cy=mxz (d.) none of these
View SolutionThe lines which intersect the skew lines y=mx,z=c;y=−mx,z=−c and the x-axis lie on the surface
a. cz=mxy b. xy=cmz c. cy=mxz d. none of these
View SolutionProve that |(b+x)(c+x)(v+x)(a+x)(a+x)(b+x)(b+y)(c+y)(c+x)(a+t)(a+y)(b+y)(b+z)(c+z)(c+z)(a+z)(a+z)(b+z)|=(b−c)(c−a)(y−z)(x−y).
View Solution
