Determine the local maxima and local minima of f(x)=x3−6x2+12x−8 isSolution in Bengali
At x=π/2,f'(x) changes sign from + ve to - ve.
y = f(x) has maxima at x=π2
At x=π,f'(x) does not change sign and f''(π)=0 as the x-axis is tangent to the curve.
x=π is the point of inflection.
At x=3π/2,f''(x) changes sign from - ve to + ve.
So y=3π/2 has minima at x=3π2.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.161videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.171videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.141videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGE PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Comprehension Type7videos
FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises18videos
GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
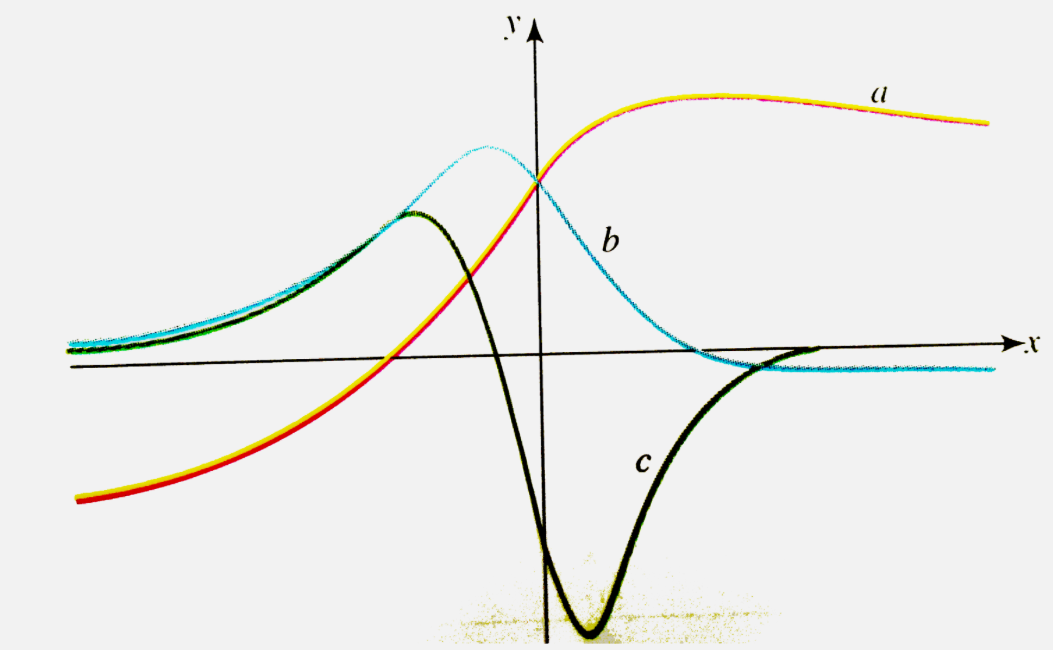
The figure shows the graphs of f, f' and f''. Indentify each curve and explain your choices.
 01:33View Solution
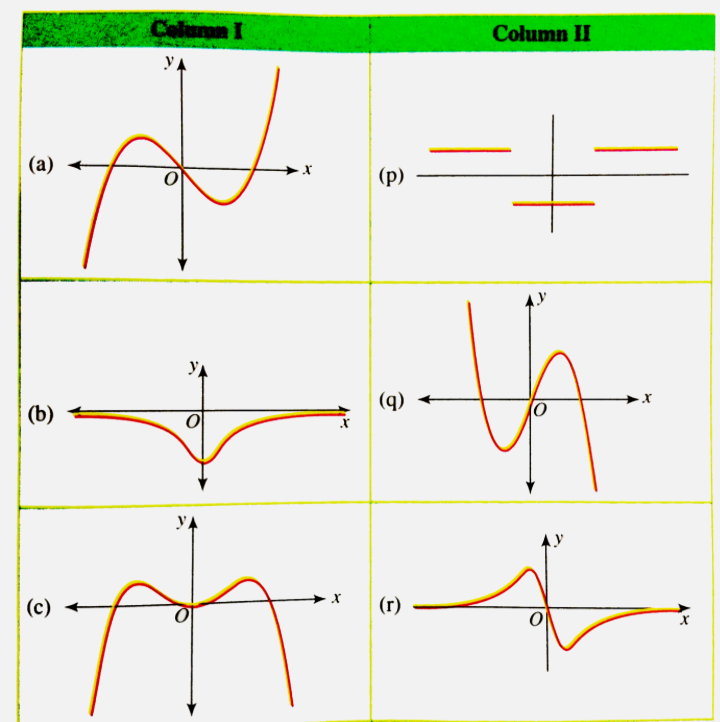
01:33View SolutionMatch the graph of y = f(x) in Column I with the corresponding graph of y = f'(x) in Column II.
 02:50View Solution
02:50View SolutionFind the intervals in which f(x)=x2+2x−5 is increasing or decreasing.
02:50View SolutionLet f(x)=x2−2x−1∀x∈R.Letf:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective.
If f:R→R, then range of values of k for which equation f(|x|)=k has 4 distinct real roots is03:01View SolutionDraw the graph of y=tan−1x−cot−1x.
04:04View SolutionFind all the points of local maxima and local minima of the function f(x)=x3−6x2+12x−8.
02:01View SolutionFind all the points of local maxima and minima of the f(x)=x3−6x2+9x−8
01:28View SolutionFind all the points of local maxima and minima of the function f(x)=x3−6x2+9x+15 .
03:26View SolutionFind all the points of local maxima and local minima of the function f(x)=x3−6x2+12x+15 .
03:45View SolutionShow that f(x) =(x3−6x2+12x−8) does not have any point of local maxima or minima . Hence draw graph
03:51View SolutionFind the points of local maxima and minima of the function f given by f(x)=x3−12x2+36x+5 .
02:10View SolutionFind the points of local maxima and local minima of the function f(x)=2x3−3x2−12x+8.
02:48View SolutionFind all the points of local maxima and local minima of the function f(x)=x3−6x2+12x−8.
03:11View SolutionFind all the points of local maxima and minima of the function f(x)=x3−6x2+9x−8 .
02:32View SolutionFind all the points of local maxima and local minima of the function f(x)=x3−6x2+12x−8 .
02:48View SolutionFind all the points of local maxima and local minima of the function f(x)=x3−6x2+12x−8.
06:20View Solution

