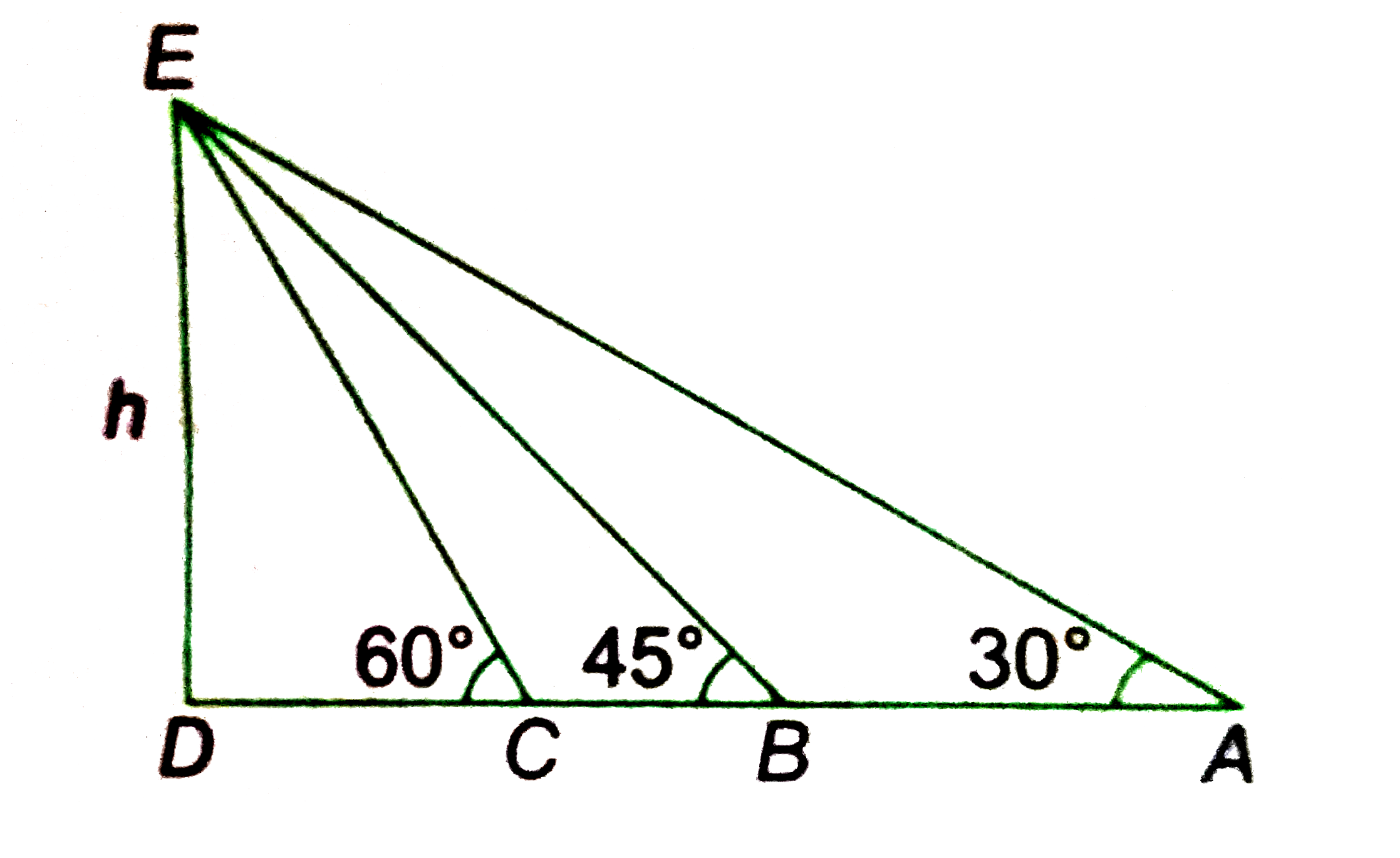
If the angles of elevation of the top of a tower from three collinear points A, B and C, on a line leading to the foot of the tower, are 300 , 450 and 600 respectively, then the ratio, AB : BC, is : (1) √3:1 (2) √3:√2 (3) 1:√3 (4) 2:3Solution in Bengali
√3:1
√3:√2
1:√3
2:3
Let ED be the tower of height h.
tan30∘=hAD
⇒AD=h√3
BD=h,CD=h√3
ABBC=AD−BDBD−CD
h√3−hh−h√3=√3−1(√3−1√3)=√3
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Exercises18videos
HIGHT AND DISTANCE
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE2videos
HYPERBOLA
Similar Questions
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30o with horizontal, then the length of the wire is (a) 12 m (b) 10 m (c) 8 m (d) 6 m
03:19View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
04:11View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 I intersect at the points A and B. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is (A) 2x−√5y−20=0 (B) 2x−√5y+4=0 (C) 3x−4y+8=0 (D) 4x−3y+4=0
02:49View SolutionA tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60^(@) at the foot of the tower,and the angle of elevation of the top of the tower from A or B is 30^(@). The height of the tower is (1) (2a)/(sqrt(3)) (2) 2a sqrt(3)(3)(a)/(sqrt(3))(4)a sqrt(3)
01:22View SolutionIf the angles of elevation of the top of a tower from three collinear points A, B and C, on a line leading to the foot of the tower, are 300 , 450 and 600 respectively, then the ratio, AB : BC, is : (1) √3:1 (2) √3:√2 (3) 1:√3 (4) 2:3
04:13View SolutionGiven b=2,c=√3,∠A=300 , then inradius of ABC is √3−12 (b) √3+12 (c) √3−14 (d) noneofthese
16:33View SolutionThe angle of elevation of the top of a tower at a point on the ground 50m away from the foot of the tower is 450. Then the height of the tower (in metres) is
05:05View SolutionIf the angles of elevation of the top of tower from three collinear points A, B and C, on a line leading to the foot of the tower, are 30∘, 45∘ and 60∘ respectively, then the ratio , AB:BC is
04:11View Solutionएक खम्भे के शीर्ष और पाद से एक टावर के शीर्ष के उन्नयन कोण क्रमश: 30∘ और 45∘ है । यदि टावर की ऊंचाई hT है और खम्भे की ऊंचाई hP है , तो निम्न में से कौन -से सही है ?
1.2hphT3+√3=h2P
2. hT−hp√3+1=hP2
3. 2(hp+hT)hP=4+√3.
नीचे दिए गए कूट का प्रयोग कर सही उत्तर चुनिए ।02:34View Solutionयदि मीनार के शीर्ष का, मीनार के पद की रेखा में स्थित तीन संरेखित बिन्दुओं A, B तथा C से उन्नयन कोण क्रमशः 30∘,45∘ तथा 60∘ हो, तब अनुपात AB : BC होगा
02:54View SolutionIf the angles of elevation of the top of a tower from three colinear points A, B and C, on a line leading to the foot of the tower, are 30∘,45∘and60∘ respectively, then the ratio, AB :BC, is :
01:08View SolutionAngles of elevatiobn of the top of a tower from three points (collinear) A,B and C on a road leading to the foot of the tower are 30∘,45∘ and 60∘ respectively .The ratio of AB to BC is
01:17View SolutionIf the angles of elevation of the top of a tower from three collinear points A, B and C, on a line leading to the foot of the tower, are 300 , 450 and 600 respectively, then the ratio, AB : BC, is : (1) √3:1 (2) √3:√2 (3) 1:√3 (4) 2:3
06:22View SolutionThe length of shadow of a tower on the plane ground is √3 times the height of the tower. The angle of elevation of sun is 450 (b) 300 (c) 600 (d) 900
06:02View SolutionThe angle of elevation of the top of a tower at a point on the ground 50m away from the foot of the tower is 450. Then the height of the tower (in metres) is 50√3 (b) 50 (c) 50√2 (d) 50√3
View SolutionA tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that A B""(=""a) subtends an angle of 60^@ at the foot of the tower, and the angle of elevation of the top of the tower from A or B is 30^@ . The height of the tower is (1) (2a)/(sqrt(3)) (2) 2asqrt(3) (3) a/(sqrt(3)) (4) asqrt(3)
03:19View Solution

