Given C1<C2<C3<C4<C5 and the function y=f(x) is twice differentiable .
f'(x)>0 for x∈(C2,C4),f'(C2)=f'(C4)=0 and f'(x)<0 for all the remaining values. Also f''(C1)=f''(C3)=f''(C5)=0 and f''(x)>0 for x∈(C1,C3)∪(C5,∞) and f''(x)<0 for remaining values. Answer the following:
(i) What is the minimum number of asymptotes parallel to the x-axis for y=f(x)?
(ii) What is the maximum number of asymptotes parallel to the x-axis of y=f(x) ?
(iii) If the range of y=f(x) is [a,b],a,b∈R, then what is the minimum number of asymptotes parallel to the x-axis of y=f(x) ?
(iv) If the range of y=f(x) is non-finite interval, then what is the maximum number of asymptotes parallel to the x-axis ?
(i) If the graph of y=f(x) is as given in the figure, it will not have any asymptote.
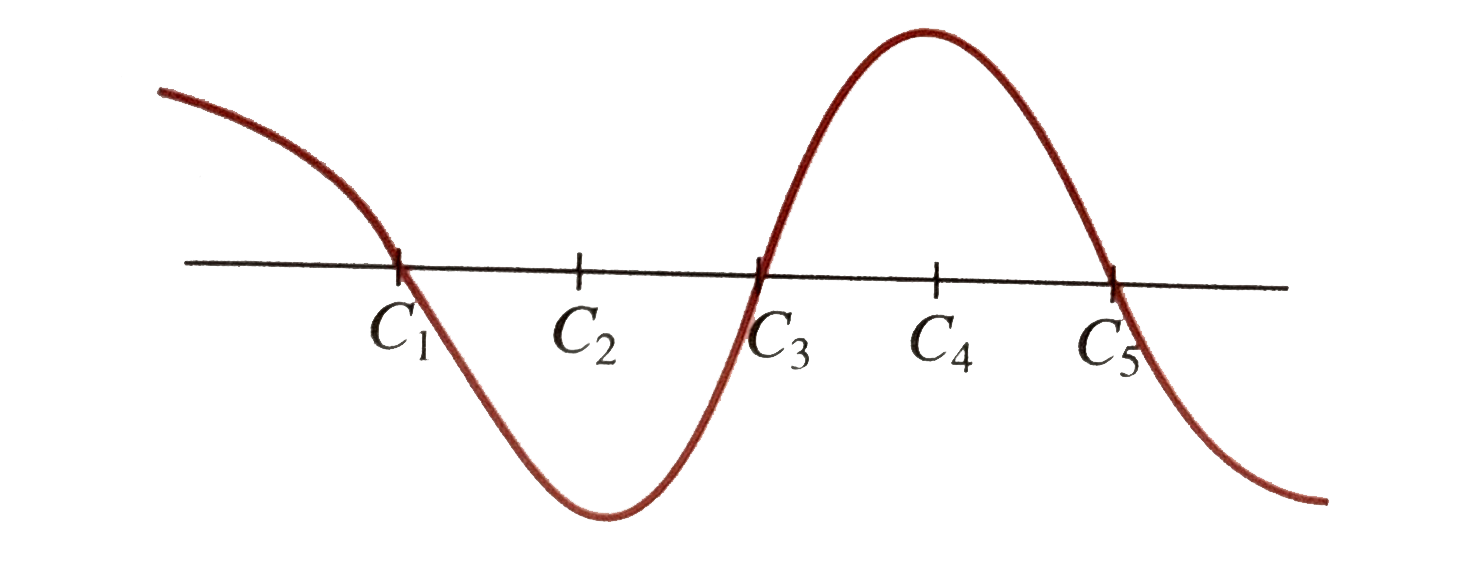
(ii) If the graph is as given in the figure, then it will have two asymptotes.
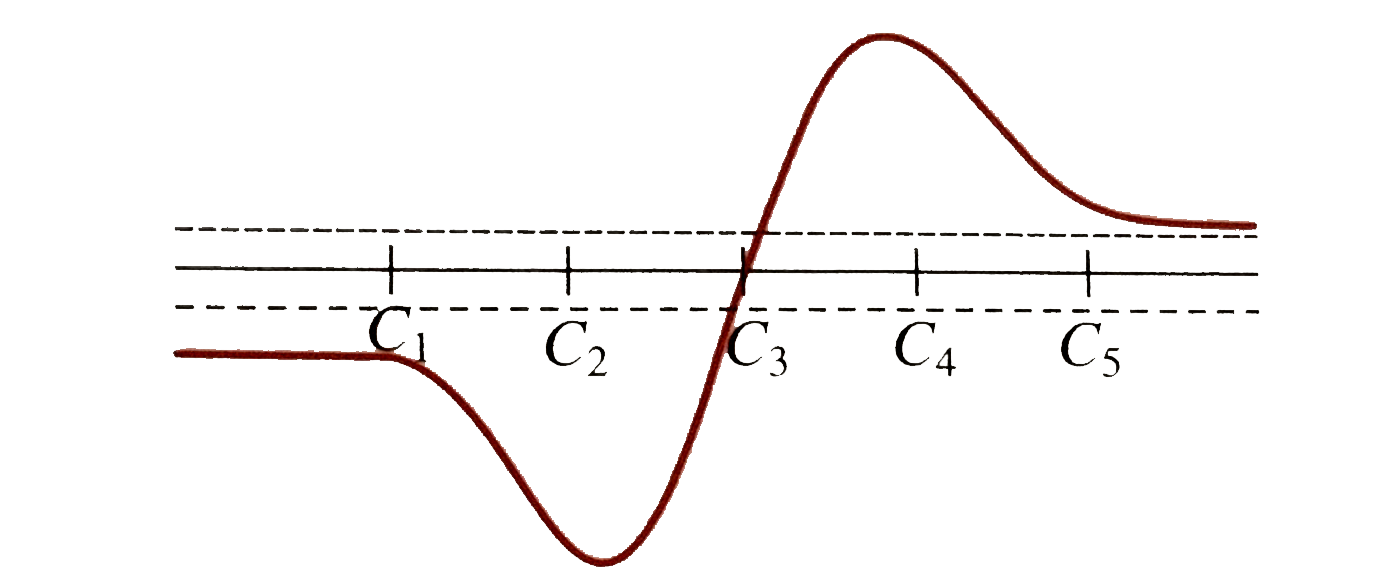
(iii) Since the range is a finite interval , the function must have at least one asymptote.
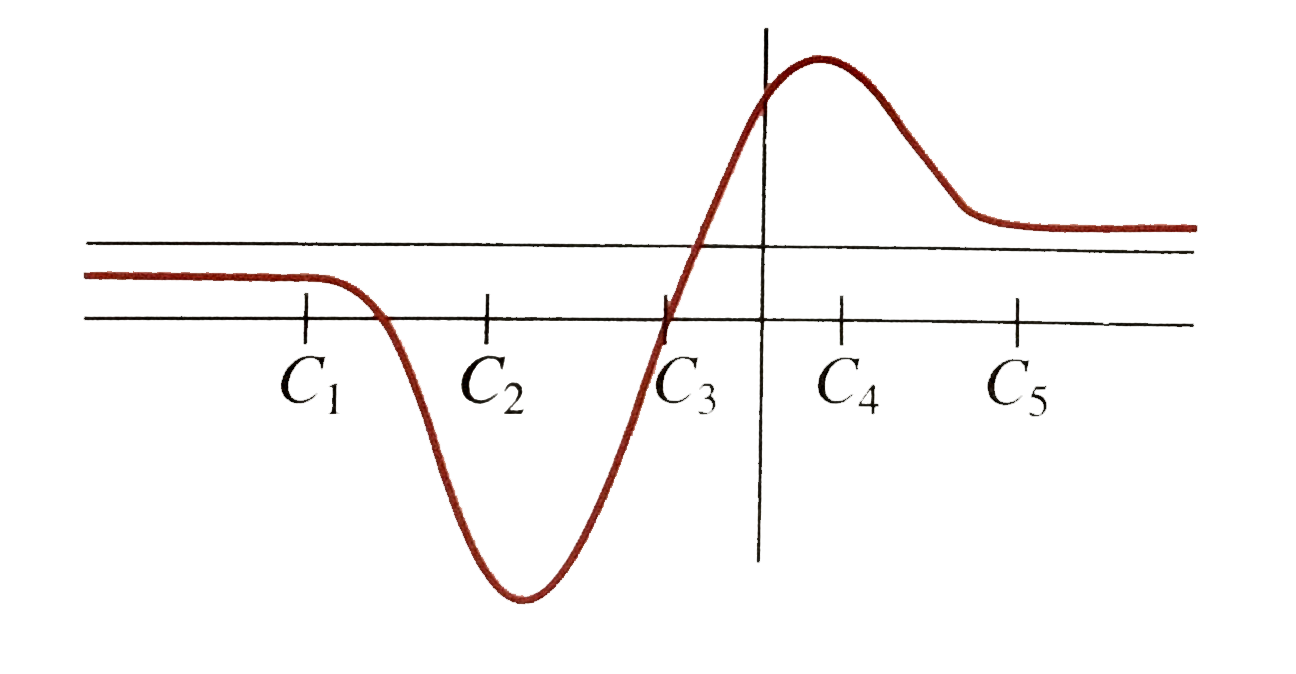
(iv) For the range to be an infinite interval, it should be non-bounded from at least one side.
So the maximum number of asymptotes is one.
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - ILLUSTRATION
78 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
Similar Questions
If f(x) is a differentiable function wherever it is continuous and f'(c1)=f'(c2)=0 f''(c1).f''(c2)<0,f(c1)=5,f(c2)=0 and (c1<c2) . If f(x) is continuous in [c1,c2] and f''(c1)−f''(c2)>0 then minimum number of roots of f'(x)=0 in [c1−1,c2+1] is
View SolutionIf a twice differentiable function f(x) on (a,b) and continuous on [a, b] is such that f''(x)<0 for all x∈(a,b) then for any c∈(a,b),f(c)−f(a)f(b)−f(c)>
View Solution
Knowledge Check
If f(c) < 0 and f'(c) > 0 , then at x = c , f (x) is -
AmaximumBminimumCneither maximum nor minimumDeither maximum or minimumIf f(x) is a differentiable function wherever it is continuous and f'(c1)=f'(c2)=0,f''(c1).f''(c2)<0,f(c1)=5,f(c2)=0and(c1<c2)
If f(x) is continuous in [c1,c2]andf''(c1)−f''(c2)<0, then minimum number of roots of f'(x)=0 in c1−1,c2+1] isA1B2C3D4If f(x) is a differentiable function wherever it is continuous and f'(c1)=f'(c2)=0,f''(c1).f''(c2)<0,f(c1)=5,f(c2)=0and(c1<c2)
If f(x) is continuous in [c1,c2]andf''(c1)−f''(c2)>0, then minimum number of roots of f'(x)=0 in [c1−1,c2+1] isA2B3C4D5
f(x) and g(x) are differentiable functions for 0≤x≤2 such that f(0)=5,g(0)=0,f(2)=8,g(2)=1. Show that there exists a number c satisfying 0<c<2 and f'(c)=3g'(c).
View SolutionIf f''(x)<0∀x∈(a,b) and (c,f(c)) is a point lying on the curve y=f(x), where a<c<b and for that value of c, f(c) has a maximum then f'(c) equals
View SolutionIf f(x) is a differentiable function wherever it is continuous and f'(c1)=f'(c2)=0,f''(c1).f''(c2)<0,f(c1)=5,f(c2)=0and(c1<c2)
If f(x) is continuous in [c1,c2] and f''(c1)−f''(c2)>0, then minimum number of roots of f(x)=0 in [c2−1,c2+1] is
View SolutionIf f(x) is twice differentiable and continuous function in x∈[a,b] also f'(x)>0 and f''(x)<0 and c in (a,b) then f(c)−f(a)f(b)−f(a) is greater than
View SolutionIf a twice differentiable function f(x) on (a,b) and continuous on [a, b] is such that f''(x)<0 for all x∈(a,b) then for any c∈(a,b),f(c)−f(a)f(b)−f(c)>
View Solution
