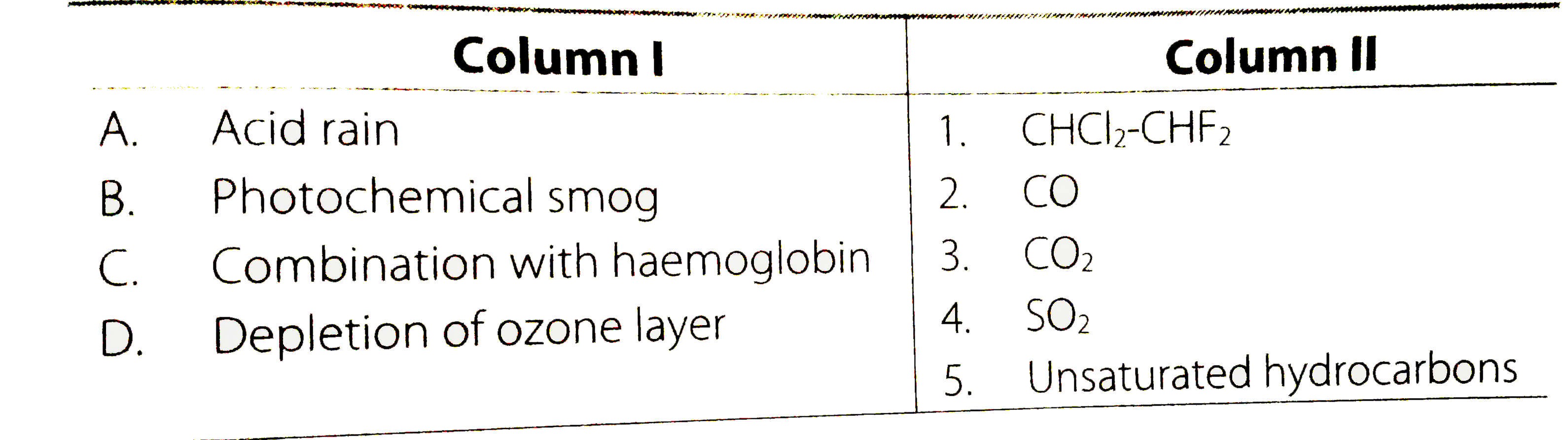
Match the terms given in Column I with the compound given in Column II.
Solution in Bengali

Video Solution

Text Solution

Verified by Experts

The correct Answer is:4

a. Let $f (x) = a x^{2} + b x (∵ f (0) = 0)$
Given $\int_{0}^{1} f (x) d x = 1$
$= 2 a + 3 b = 6$
$= (a, b) = (0, 2)$ and $(3, 0)$
b. $f (x) = sin (x^{2}) + cos (x^{2})$
$= \sqrt{2} cos (x^{2} - \frac{π}{4})$
For maximum value $x^{2} - \frac{π}{4} = 2 n π, n ε Z$
$\Rightarrow x^{2} = 2 n π + \frac{π}{4}, n ε Z$
$\Rightarrow x = \pm \sqrt{\frac{x}{4}} \pm \sqrt{\frac{9 π}{4}}$ as $x ε [- \sqrt{13}, \sqrt{13}]$
c. $I = \int_{- 2}^{2} \frac{3 x^{2}}{(1 + e^{x})} d x$ ...............1
$= \int_{- 2}^{2} \frac{3 {(- x)}^{2}}{1 + e^{- x}} d x$
$∴ I = \int_{- 2}^{2} \frac{e^{x} {(3 x)}^{2}}{e^{x} + 1} d x$ ............2
Addding 1 and 2
$\Rightarrow I + I = \int_{- 2}^{2} \frac{3 x^{2}}{(1 + e^{x})} d x + \int_{- 2}^{2} \frac{e^{x} (3 x^{2})}{e^{x} + 1} d x$
$= \int_{- 2}^{2} 3 x^{2} d x = 2 \int_{0}^{2} 3 x^{2} d x = 16$
$\Rightarrow I = 8$
d. We have $I = \frac{\int_{1 / 2}^{1 / 2} cos 2 x . log (\frac{1 + x}{1 - x}) d x}{\int_{0}^{1 / 2} cos 2 x . log (\frac{1 + x}{1 - x}) d x}$
Let $f (x) = cos 2 x I (\frac{1 + x}{1 - x})$
$∴ f (- x) = cos (- 2 x) I n (\frac{1 - x}{1 + x})$
$= - cos (2 x) I n (\frac{1 + x}{1 - x}) = - f (x)$
Thus, $f (x)$ is an odd function.
$\Rightarrow I = 0$

|

Updated on:21/07/2023

Class 12 MATHS DEFINITE INTEGRAL

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-DEFINITE INTEGRATION -JEE ADVANCED

Home
Ask Doubt
Profile