Line segment AB of fixed length c slides between coordinate axes such that its ends A and B lie on the axes. If O is origin and rectangle OAPB is completed, then show that the locus of the foot of the perpendicular drawn from P to AB is x23+y23=c23.Solution in Bengali
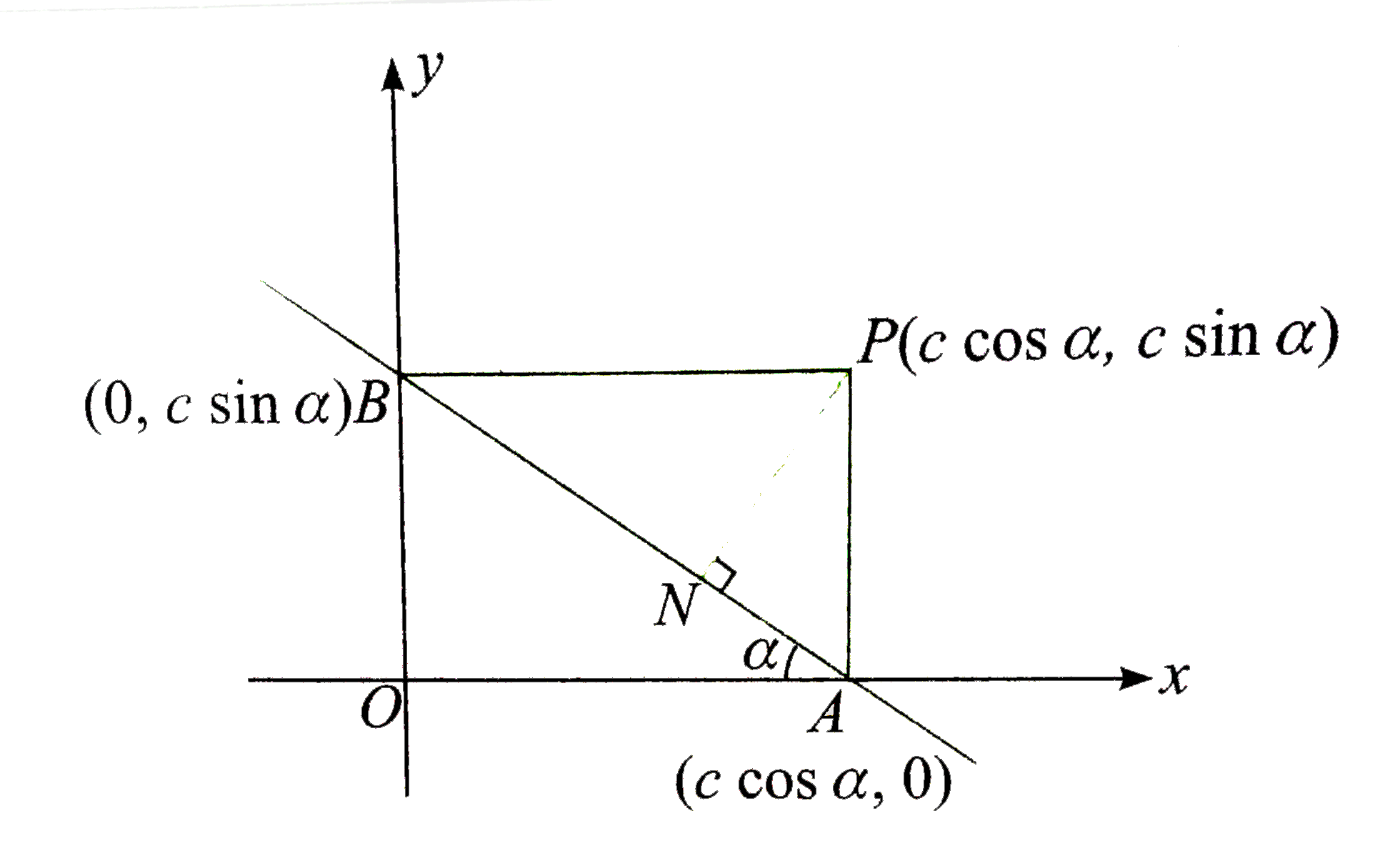
As shown in the figure, is on x-axis and B is on y-axis.
AB=c (given)
Given that OAPB is a rectangle.
Let ∠BAO=α
∴OA=ccos αandOB= c sin α
∴P≡(ccos α,csin α)
Equation of AB is
xc cos α+ycsin α=1
orxsin α+ycosα=c sinαcosα (1)
Equation of PN (perpendicular from P to AB) is
y−csinα=cota(x−ccosα)
⇒xcosα−ysinα=c(cos2α−sin2α) (2)
N is point of intersection of (1) and (2).
Solving (1) and (2), we get
x=ccos3α,y=csin3α
∴cosα=(xc)1/3,sinα=(yc)1/3
Squaring and adding, we get
(xc)2/3+(yc)2/3=1
orx2/3+y2/3=c2/3,which is the required locus
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXAMPLE12videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.123videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
Show that the lines 4x+y−9=0,x−2y+3=0,5x−y−6=0 make equal intercepts on any line of slope 2.
05:43View SolutionFind the equation of the right bisector of the line segment joining the points (3,4) and (-1,2).
09:06View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
03:55View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
09:18View SolutionA rod of length k slides in a vertical plane, its ends touching the coordinate axes. Prove that the locus of the foot of the perpendicular from the origin to the rod is (x2+y2)3=k2x2y2.
11:40View SolutionThe ends A and B of a straight line segment of constant length c slide upon the fixed rectangular axes OX and OY ,respectively.If the rectangle OAPB be completed,then the locus of the foot of the perpendicular drawn from P to AB is
14:26View SolutionIf AB is the intercept of the tangent to the circle x^(2)+y^(2)=r^(2) between the coordinate axes,the locus of the vertex P of the rectangle OAPB is
02:47View SolutionLine segment AB of fixed length c slides between coordinate axes such that its ends A and B lie on the axes. If O is origin and rectangle OAPB is completed, then show that the locus of the foot of the perpendicular drawn from P to AB is x23+y23=c23.
04:02View SolutionThe circle A and B of a line segment of constant length c unit slides upon the fixex rectangular axes OX and OY. If P be a point on the plane such that OAPB is a rectangle, then show that locus of the foot of the perpendicular drawn from P to AB is x2/3+y2/3=c2/3.
07:04View Solutionअचर लम्बाई c के रेखा खण्ड के सिरे A एवं B क्रमशः समकोणीय अक्षों OX एवं OY पर फिसलते है। यदि आयत OAPB बनाया जाता है, तब प्रदर्शित कीजिए कि बिन्दु P से AB पर डाले गये लम्ब के पाद का बिन्दु पथ x23+y23=c23 है।
06:51View SolutionA straight line of length 3 units slides with its ends A,B always on X and Y axes respectively.If locus of centroid of ΔOAB is ax2+by2=c then a+b+c=
06:44View SolutionHyperbola x^2/a^2-y^2/b^2=1 Any point of P The tangent line drawn on the coordinates on the axes respectively A and B Bites on. If quadrilateral OAPB Where there is a rectangle O Is the pivot, then P Is a locus of
14:26View SolutionA rod of length k slides in a vertical plane, its ends touching the coordinate axes. Prove that the locus of the foot of the perpendicular from the origin to the rod is (x2+y2)3=k2x2y2.
09:08View SolutionThe ends A and B of a straight line segment of constant length c slide upon the fixed rectangular axes OX and OY, respectively. If the rectangle OAPB be completed, then the locus of the foot of the perpendicular drawn from P to AB is
08:35View SolutionA rod of length k slides in a vertical plane, its ends touching the coordinate axes. Prove that the locus of the foot of the perpendicular from the origin to the rod is (x2+y2)3=k2x2y2.
03:10View SolutionThe ends A and B of the line segment of constant length are sliding on right-angled axes OX and OY respectively. If the rectangle OAPB is drawn, then demonstrate that the point path of the foot of the perpendicular from point P to AB x^(23) +y^(23) = c^(23) is.
06:34View Solution

