Question

The lines $y=m_{1}x,y=m_{2}xandy=m_{3}x$
make equal intercepts on the line $x+y=1.$
Then
$2(1+m_1)(1+m_3)=(1+m_2)(2+m_1+m_3)$

$(1+m_1)(1+m_3)=(1+m_2)(1+m_1+m_3)$

$(1+m_1)(1+m_2)=(1+m_3)(2+m_1+m_3)$

$2(1+m_1)(1+m_3)=(1+m_2)(1+m_1+m_3)$

Options

A. `2(1+m_(1))(1+m_(3)) = (1+m_(2))(2+m_(1)+m_(3))`
B. `(1+m_(1))(1+m_(3)) = (1+m_(2))(1+m_(1)+m_(3))`
C. `(1+m_(1))(1+m_(2)) = (1+m_(3))(2+m_(1)+m_(3))`
D. `2(1+m_(1))(1+m_(3)) = (1+m_(2))(1+m_(1)+m_(3))`

Answer

A

Explanation

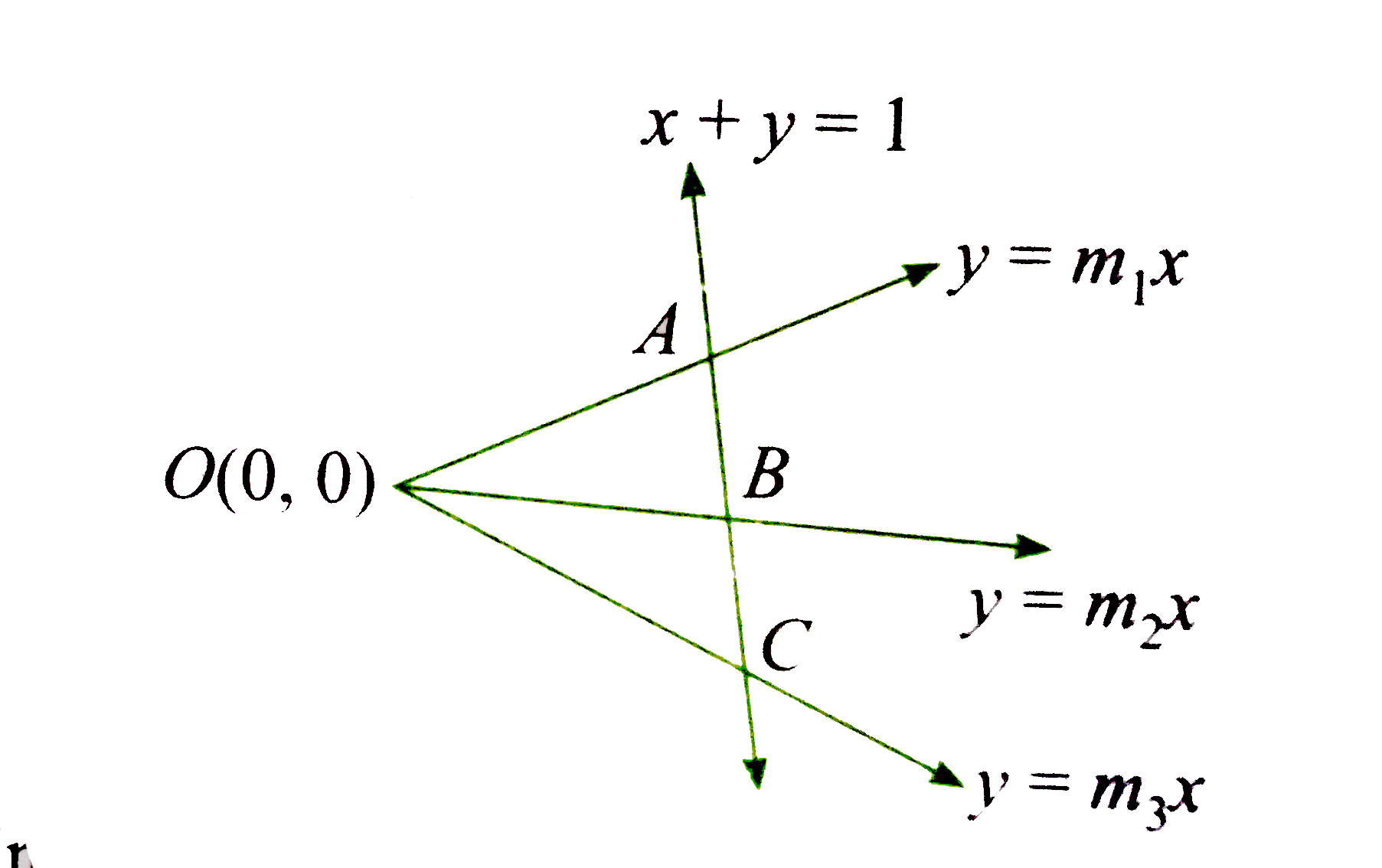
Solving the equations of the lines, we get
`A-=((1)/(1+m_(1)),(m_(1))/(1+m_(1))),C-=((1)/(1+m_(3)),(m_(3))/(1+m_(3)))`
If AB=BC, then the midpoint of AC lies on
`y=m_(2)x`
`"or "(m_(1)/(1+m1)+(m_(3))/(1+m3))/(2) = m_(2)[((1)/(1+m_(1))+(1)/(1+m_(3)))/(2)]`