The equation of the bisector of the acute angle between the lines 2x−y+4=0 and x−2y=1 is Solution in Bengali
x+y+5=0
x-y+1=0
x-y=5
none of these
The correct Answer is:B
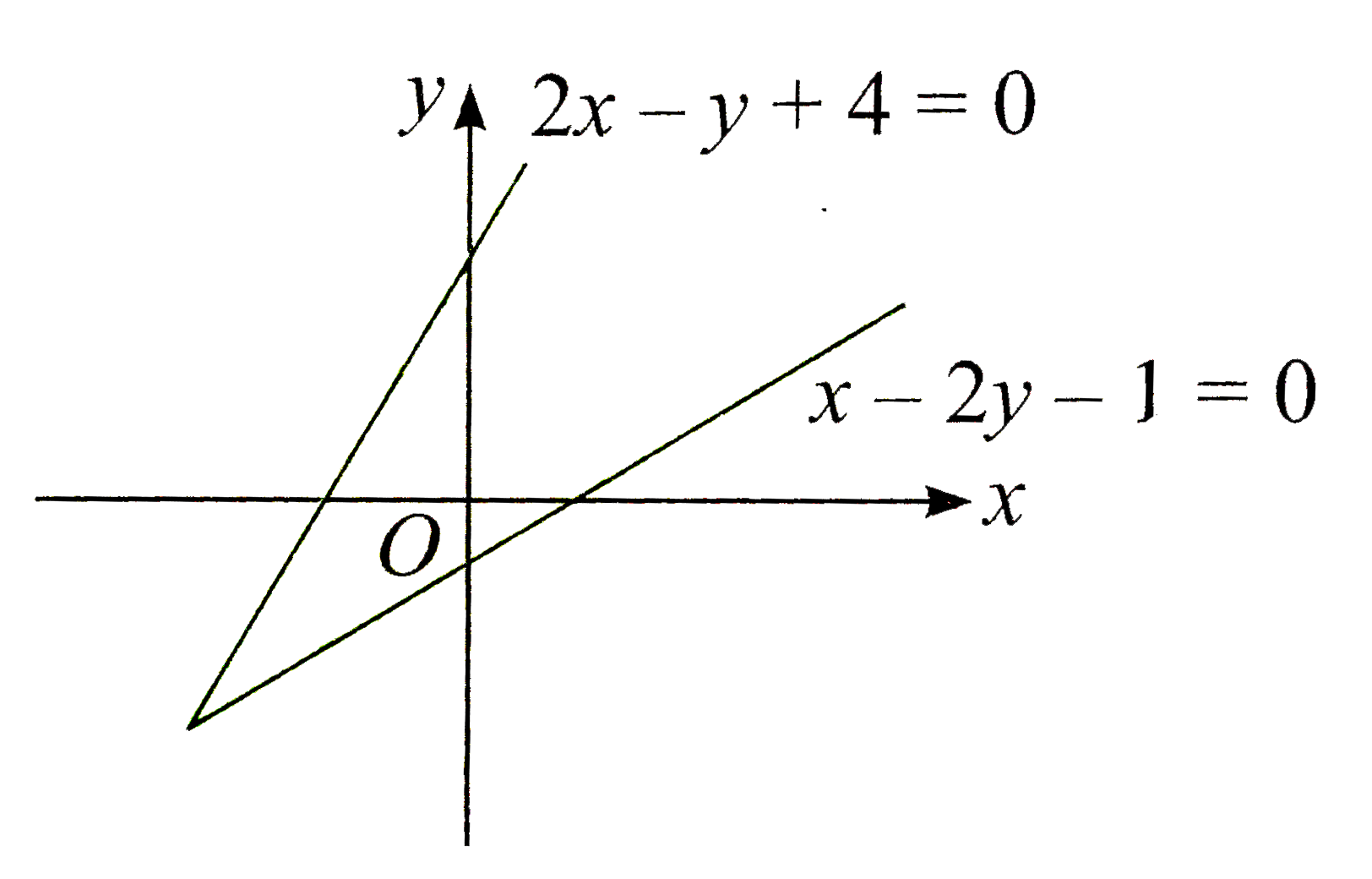
Clearly, from the figure, the origin is contained in the acute angle. Writing the equations of thel lines as 2x-y+4=0 and -x+2y+1=0, the required bisector is
2x−y+4√5=−x+2y+1√5
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)30videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
05:42View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
02:05View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
02:02View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
02:18View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
04:45View SolutionThe equation of the bisector of the obtuse angle between the lines x-2y+4=0 and 4x-3y+2=0 is
08:21View SolutionThe equation of the bisector of the acute angle between the lines 2x−y+4=0 and x−2y=1 is (a) x−y+5=0 (b)x−y+1=0 (c)x−y=5 (d) none of these
03:42View SolutionBisector of angle between x+2y-1=0 and 2x+y+1=0 containing (2,1) is
04:36View SolutionFor the straight lines 2x−y+1=0 and x−2y−2=0 find the equation of the
(i) bisector of the obtuse angle between them ,
(ii) bisector of the acute angle between them ,10:01View SolutionFind the bisector of acute angle between the lines x+y−3=0and7x−y+5=0
06:58View Solutionरेखाओं x-2y+4 = 0 तथा 4x -3y + 2 = 0 के बीच के अधिककोण के अर्द्धक का समीकरण निकालें।
02:53View SolutionFind the equations of the bisectors of the angles formed by the following pairs of lines
x+2y+3=0 and 2x+y−2=005:38View SolutionThe equation of the bisector of the acute angle between the lines 2x−y+4=0 and x−2y=1 is (a) x−y+5=0 (b)x−y+1=0 (c)x−y=5 (d) none of these
06:29View SolutionObtain the equation of the bisector of the acute angle between the pair of lines. X + 2y = 1 , 2x + y + 3 = 0
05:23View SolutionFind the equation-of the bisector of the obtused angle between the straight lines x-2y+4=0 and 4x-3y+2=0.
04:28View Solution

