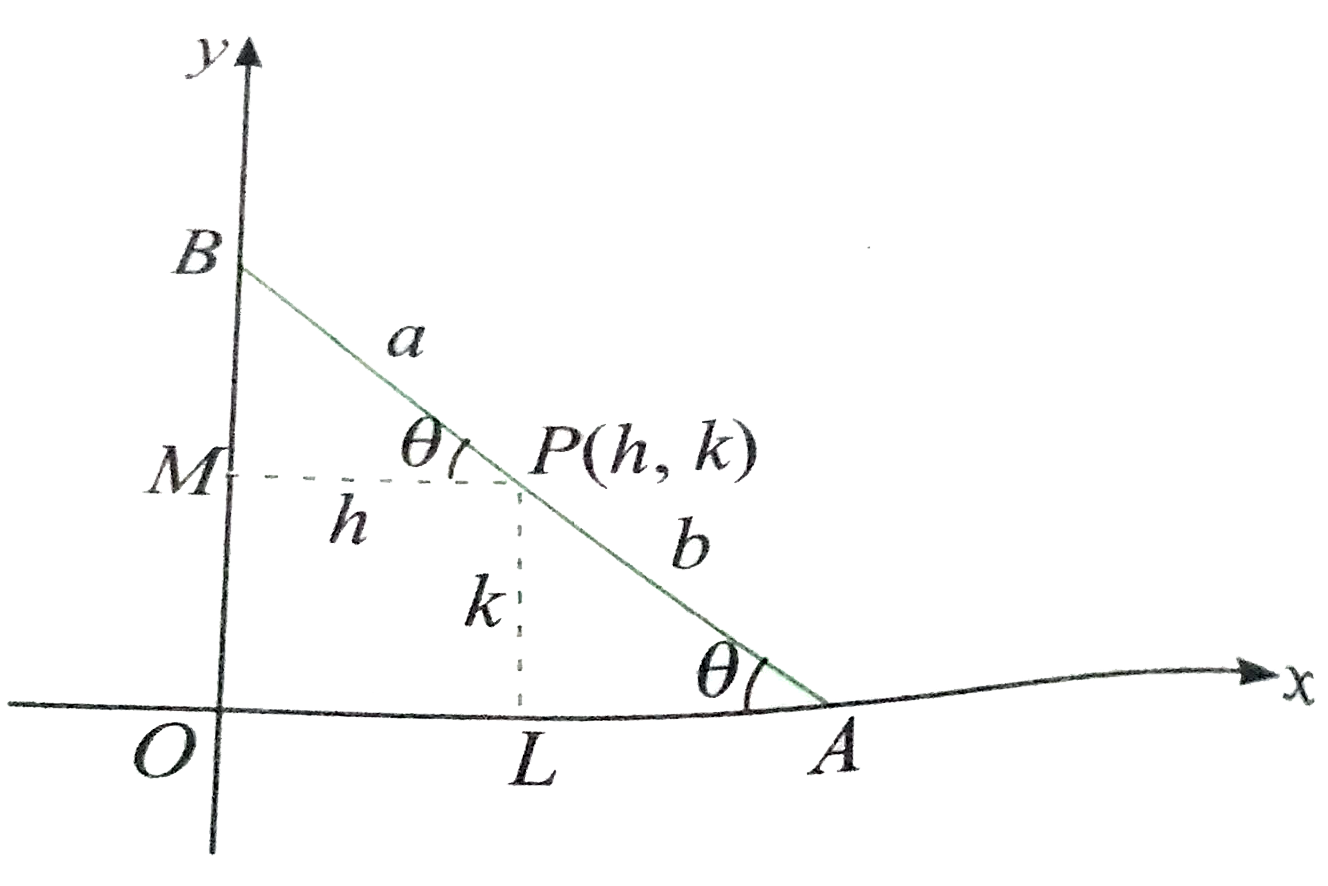
AB is a variable line sliding between the coordinate axes in such a way that A lies on the x-axis and B lies on the y-axis. If P is a variable point on AB such that PA=b,Pb=a , and AB=a+b, find the equation of the locus of P.Solution in Bengali
Let P(h,k) be a variable point on AB such that ∠OAB=θ.
Here, θ is a variable from triangles ALP and PMB.we have
sinθ=kb (1)
cosθ=ha (2)
Here, θ is a variable so, we have to elimiante θ. Squareing (1) and (2) and adding, we get
k2b2+h2a2=1
x2a2+y2b2=1
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.631videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.641videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.611videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Two points PandQ are given. R is a variable point on one side of the line PQ such that ∠RPQ−∠RQP is a positive constant 2α. Find the locus of the point R.
01:43View SolutionIf the coordinates of a variable point P are (acosθ,bsinθ), where θ is a variable quantity, then find the locus of P.
01:10View SolutionFind the locus of a point such that the sum of its distance from the points (0, 2) and (0,−2) is 6.
05:02View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
03:23View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
01:16View SolutionAB is a variable line sliding between the coordinate axes in such a way that A lies on the x-axis and B lies on the y-axis. If P is a variable point on AB such that PA=b,Pb=a , and AB=a+b, find the equation of the locus of P.
06:19View SolutionIf the coordinates of a variable point P are (acosθ,bsinθ), where θ is a variable quantity, then find the locus of P.
View SolutionFor a variable line (x)/(a)+(y)/(b)=1,a+b=10 the locus of mid point of the intercept of this line between coordinate axes is
03:22View SolutionA is any point on X -axis and B is any point of Y- axis and P is a variable point on AB with PA=b and PB=a and AB=a+b. Find the equation of locus of P
05:11View SolutionIf the coordinates of a variable point P be (acosθ,bsinθ), where θ is a variable quantity, find the locus of P.
04:42View Solutionमाना एक रेखाखण्ड AB की लम्बाई a+b है | वह इस प्रकार गति करता है कि इसके सिरे A तथा B सदैव x-अक्ष तथा y-अक्ष पर रहते है | AB पर एक चर बिन्दु P का बिन्दुपथ ज्ञात कीजिए जिसके लिए PA=a,PB=b
06:47View SolutionA rod AB of length 15 cm rests in between two coordinate axes is such a way that the end point A lies on x-axis and end Point B lies on y-axis. A point P (x,y) is taken on the rod in such a way that AP=6cm . Show that the locus of P is an ellipse.
03:16View SolutionA rod AB of length 15 cm rests in between two coordinate axes is such a way that the end point A lies on x-axis and end Point B lies on y-axis. A point P (x,y) is taken on the rod in such a way that AP=6cm . Show that the locus of P is an ellipse.
05:47View SolutionA rod AB of length 15 cm rests in between two coordinate axes is such a way that the end point A lies on x-axis and end Point B lies on y-axis. A point P (x,y) is taken on the rod in such a way that AP=6cm . Show that the locus of P is an ellipse.
07:01View SolutionA rod AB of length 15 cm rests in between two coordinate axes is such a way that the end point A lies on x-axis and end Point B lies on y-axis. A point P (x,y) is taken on the rod in such a way that AP=6cm . Show that the locus of P is an ellipse.
03:18View SolutionAB is a variable line sliding between the coordinate axes in such a way that A lies on the x-axis and B lies on the y-axis. If P is a variable point on AB such that PA=b,Pb=a , and AB=a+b, find the equation of the locus of P.
06:41View Solution

