Find the locus of the middle point of the portion of the line $x cos α + y sin α = p$ which is intercepted between the axes, given that $p$ remains constant.Solution in Bengali

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{1}{x^{2}} + \frac{1}{y^{2}} = \frac{4}{p^{2}}$

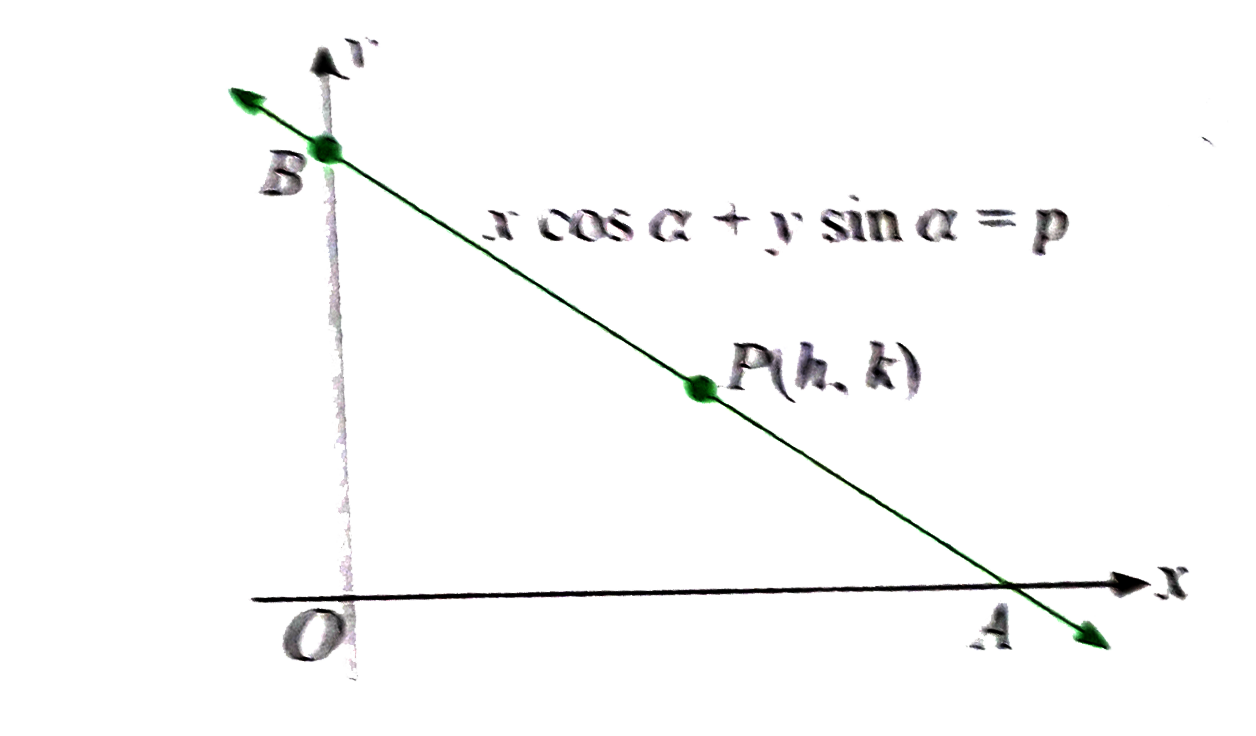
The equation of the variable line is $x cos α + y sin α = p$
Here P is a constant and $α$ is the parameter (variable),
Let the line in (1) cuts- x and y-axes at A and B respectively,
Putting $y = 0$ in (1) , we get $A \equiv (p sec α, 0)$
Putting $x = 0$ in (1) we get $B \equiv (0, p cos e c α)$ .
AB is the portion of (1) intercepted between the axes.
Let P(h,k) be the midpoint of AB. we have to find the locus of pont (h,k) for this, we will to eliminate $α$ and find a relation in h and k. Therefore.
$h = \frac{p sec α + 0}{2} = \frac{p}{2} sec α (2)$
and $k = \frac{0 + p cos e c α}{2} = \frac{p}{2} cos e c α$
From (2) , we get
$cos α = \frac{p}{2 h}$
From (3)we get
$sin α = \frac{p}{2 k}$
or ${cos}^{2} α + {sin}^{2} α = \frac{p^{2}}{4 h^{2}} + \frac{p^{2}}{4 k^{2}}$
or $\frac{1}{h^{2}} + \frac{1}{k^{2}} = \frac{4}{p^{2}}$
Hence,the locus of pont P(h,k) is $\frac{1}{x^{2}} + \frac{1}{y^{2}} = \frac{4}{p^{2}}$ .

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-COORDINATE SYSYEM -Concept applications 1.6

Home
Ask Doubt
Profile