Match the following lists and then choose the correct code.

A
abcdprqq
B
abcdqprs
C
abcdspqr
D
abcdrsqp
Text Solution
The correct Answer is:B
2
a. We get common normal perpendicular to y=x.
So, slope =−1⇒x+y=3a
b. Tangent to the parabola y=mx+a/m passes through the point P(h,k).
⇒m2h−mk+a=0
If its roots are m1andm2, then m1m2−+1
Thus, locus is x=a.
c. The tangents are
y=m(x+a)+a/m (1)
andy=−1m(x+2a)−2am (2)
Subtracting (1) from (2), we get
x+3a=0
d. If chord joining t1andt1 subtends angle of 90∘ at vertex then t1t2=−4. Point of intersection of tangents is (−at1t1,−a(t1+t1)). So, the locus is x=4a.
|
Topper's Solved these Questions
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - NUMERICAL VALUE TYPE
32 Videos
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - ARCHIVES SINGLE CORRECT ANSWER TYPE
8 Videos
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - LINKED COMPREHENSION TYPE
45 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGE PUBLICATIONCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension
8 Videos
Similar Questions
Knowledge Check
Match the following lists and and then choose the correct code.

 AabcdprqqBabcdqprsCabcdspqrDabcdrsqp
AabcdprqqBabcdqprsCabcdspqrDabcdrsqpMatch the following column and choose the correct code
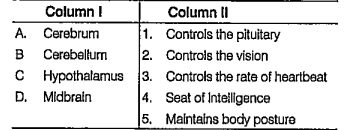 A
A B
B C
C D
D
Match the following two lists and choose the correct answer from the codes given below:
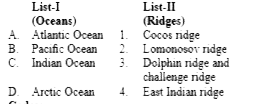 AA-2,B-4,C-1,D-3BA-3,B-1,C-4,D-2CA-1,B-2,C-3,D-4DA-4,B-3,C-2,D-1
AA-2,B-4,C-1,D-3BA-3,B-1,C-4,D-2CA-1,B-2,C-3,D-4DA-4,B-3,C-2,D-1
Match the following columns and choose the correct code.

View SolutionMatch the following two lists and choose the correct answer from the codes given below:
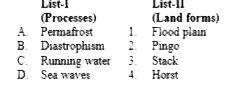
View SolutionMatch the relation for derivatives given in List II with the relation given in List I and then choose the correct code.

View SolutionMatch List I with List II and choose the correct code
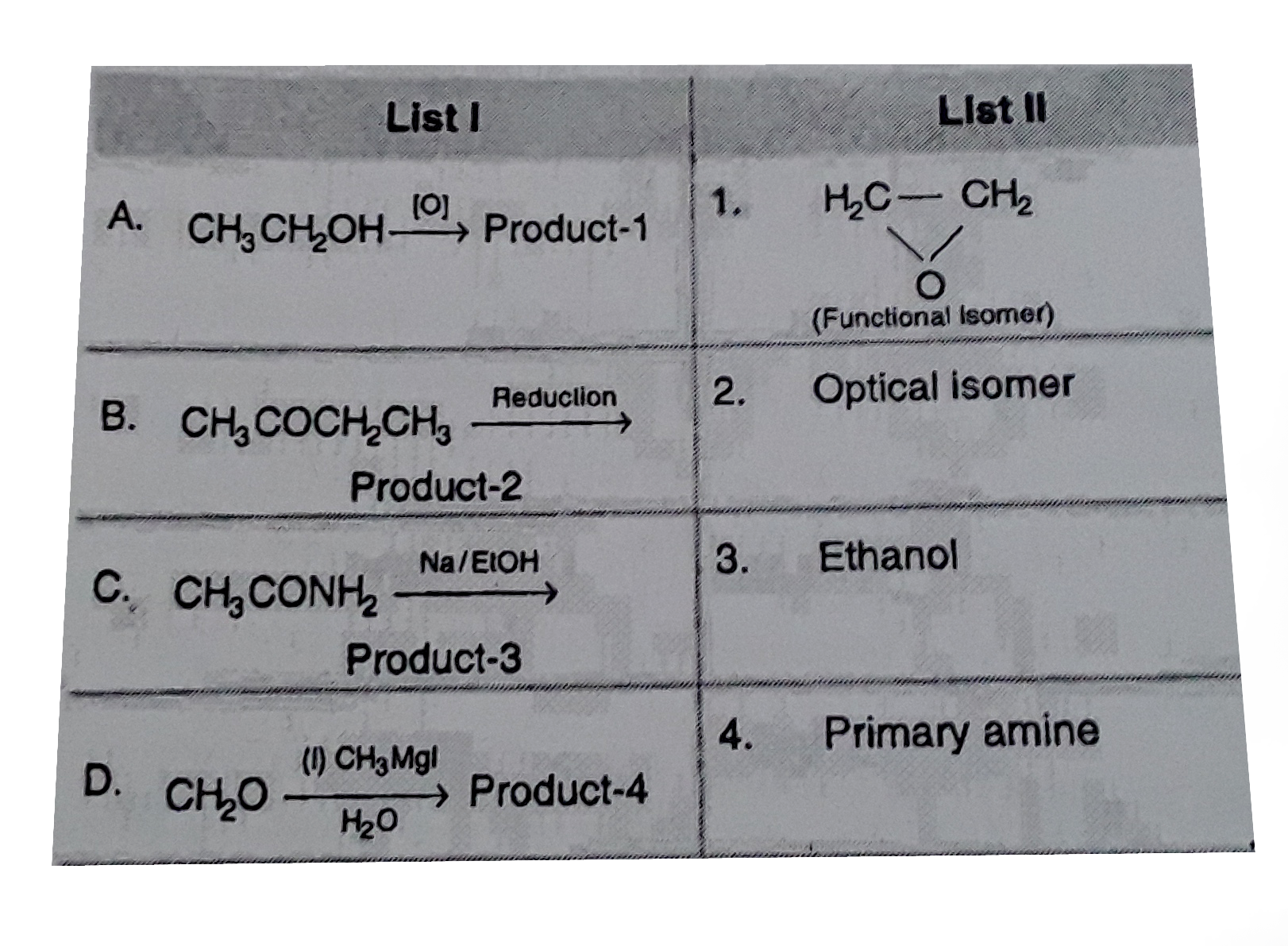
View SolutionMatch the columns and choose the correct code.

View Solution


