Let P be a point interior to the acute triangle ABC. If PA+PB+PC is a null vector, then w.r.t traingel ABC, point P is its a. centroid b. orthocentre c. incentre d. circumcentreSolution in Bengali
centroid
orthocentre
incentre
circumcentre
The correct Answer is:a
→a−→p+→b−→p+→c−→p=0
or→p=→a+→b+→c3
Hence, P is centroid .
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Reasoning type
8 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Comprehension type
27 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercises
15 Videos
- DETERMINANTSBOOK - CENGAGE PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - All Questions
262 Videos
- DIFFERENTIAL EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - All Questions
578 Videos
Similar Questions
Statement 1: Vector →c=−5ˆi+7ˆj+2ˆk is along the bisector of angel between →a=ˆi+2ˆj+2ˆkand→b=8ˆi+ˆj−4ˆk. Statement 2: →c is equally inclined to →aand→b.
View SolutionLet →u,→vand→w be three unit vectors such that →u+→v+→w=→a,→u×(→v×→w)=→b,(→u×→v)×→w=→c,→a.→u=3/2,→a.→v=7/4and|→a|=2
Vector →w is
View SolutionShow that
∣∣ ∣ ∣∣(a−x)2(a−y)2(a−z)2(b−x)2(b−y)2(b−z)2(c−x)2(c−y)2(c−z)2∣∣ ∣ ∣∣=2(a−b)(b−c)(c−a)(x−y)(y−z)(z−x)
View SolutionIf P = {1,2}, form set set P×P×P
View SolutionFor each of the following differential equations verify that the accompanying functions a solution. Differential Function
(a)xdydx=y, y=ax
(b)x+ydydx=0, y=±√a2−x2
(c)xdydxy=y2, y=ax+a
(d)x3d2ydx2=1, y=ax+b+12x
(e)y=(dydx)2, y=14(x±a)2
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
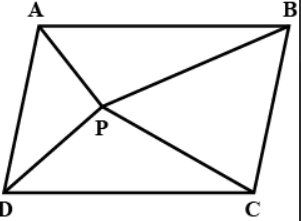
View SolutionLet P be a point interior to the acute triangle ABC. If PA+PB+PC is a null vector, then w.r.t traingel ABC, point P is its a. centroid b. orthocentre c. incentre d. circumcentre
View SolutionLet ABC be a triangle whose circumcentre is at P. If the position vectors of A,B,C and P are bar(a),bar(b),bar(c) and (bar(a)+bar(b)+bar(c))/(4) respectively then the positive vector of the orthocentre of the triangle is
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)
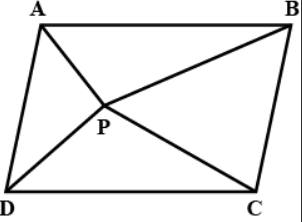
View SolutionIf (a,b),(x,y),(p,q) are the coordinates of circumcentre,centroid,orthocentre of the triangle then
View SolutionLet ABC be a triangle whose circumcentre is at P. If the position vectors of A, B, C and P are →a,→b,→cand→a+→b+→c4
respectively, then the position vector of the orthocentre of this triangle is
View Solutionlet P an interioer point of a triangle ABC and AP,BP,CP meets the sides BC,CA,AB in D,E,F, respectively, Show that APPD=AFFB+AEEC.
View SolutionLet P be a point interior to the acute triangle ABC. If PA+PB+PC is a null vector, then w.r.t traingel ABC, point P is its a. centroid b. orthocentre c. incentre d. circumcentre
View SolutionLet P be a point interior to the acute triangle ABC. If PA+PB+PC is a null vector, then w.r.t traingel ABC, point P is its a. centroid b. orthocentre c. incentre d. circumcentre
View SolutionLet P be a point interior to the acute triangle ABC. If PA+PB+PC is a null vector, then w.r.t traingel ABC, point P is its a. centroid b. orthocentre c. incentre d. circumcentre
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.andCP∣∣AB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.
View Solution
