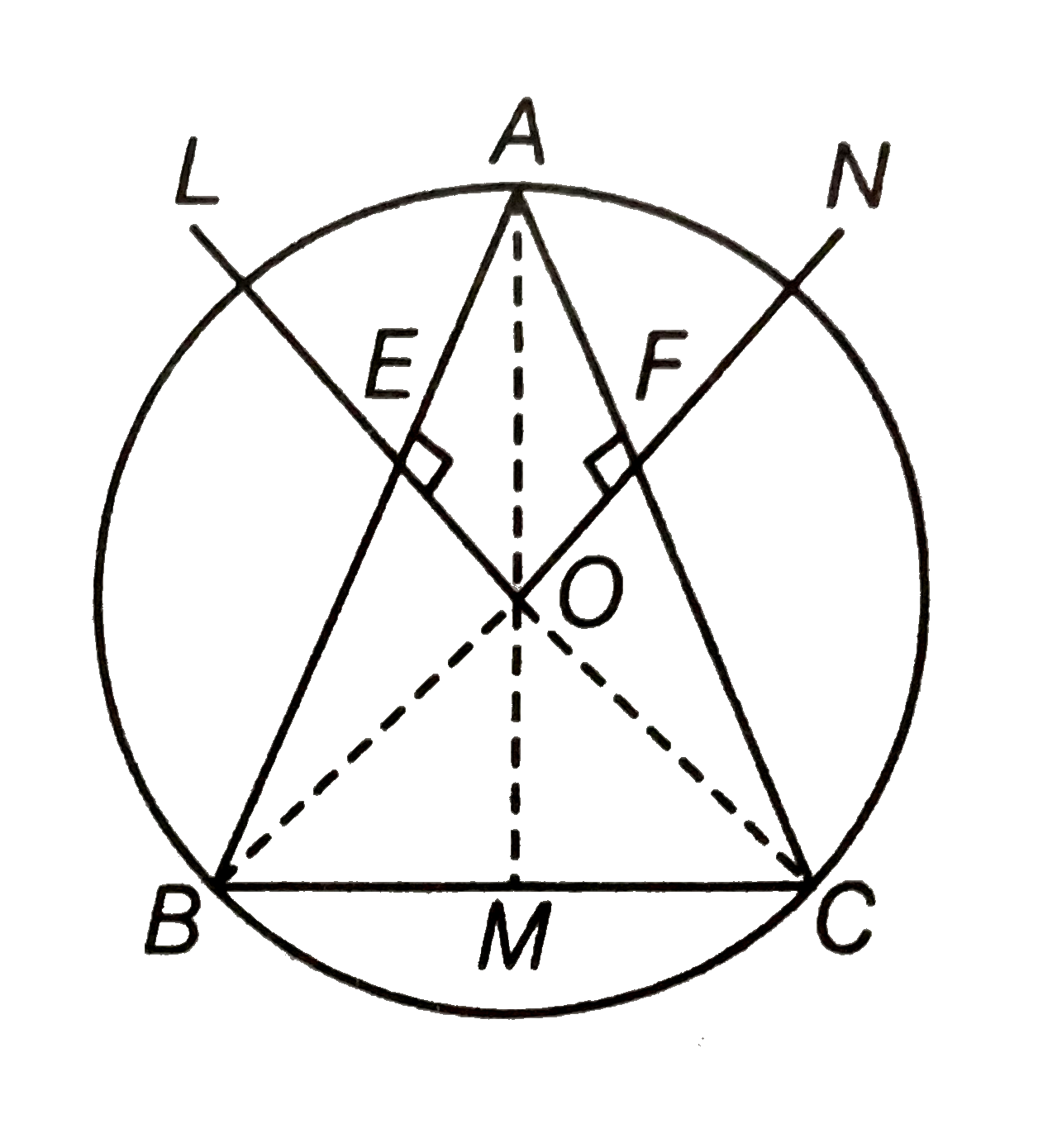
from a point O inside a triangle ABC, perpendiculars, OD, OE and OF are drawn to the sides, BC, CA and AB respectively , prove that the perpendiculars from A, B and C to the sides EF, FD and DE are concurrent.
Let the position vectors of points A,B,C,D,E and F be →a,→b,→c,→d,→eand→f w.r.t O. Let perpendiculars from A to EF and from B to DF meet each other at H. let position vectors of H be →r. We join CH. In order to prove the statement given in the question. it is sufficient it is sufficient to prove that CH is prependicular to DE.
Now asOD⊥BC⇒→d.(→b−→c)=0
⇒→d.→b=→d.→c
asOE⊥AC⇒→e.(→c−→a)=0⇒→e.→c=→e.→a
as OF⊥AB⇒→f.(→a−→b)=0⇒→f.→a=→f.→b
Also AH⊥EF⇒(→r.→a).(→e−→f)=0
⇒→r.→e−→r.→f−→a.→e+→a.→f=0
andBH⊥FD⇒(→r−→b).(→f−→d)=0
⇒→r.→f−→r.→d−→b.→f+→b.→d=0
Adding (iv) and (v) , we get
→r.→e−→a.→e+→a.→f−→r.→d−→b.→f+→b.→d=0
or→r.(→e.→d)−→e.→c+→d.→c=0 [ using (i), (ii) and (iii))]
or(→r−→c).(→e−→d)=0
⇒−−→CH.−−→ED=0⇒CH⊥ED
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - fill in the blanks
14 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - True and false
3 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Integer type
17 Videos
- DETERMINANTSBOOK - CENGAGE PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - All Questions
262 Videos
- DIFFERENTIAL EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - All Questions
578 Videos
Similar Questions
From a point O inside a triangle ABC, perpendiculars OD,OEandOf are drawn to rthe sides BC,CAandAB, respecrtively. Prove that the perpendiculars from A,B,andC to the sides EF,FDandDE are concurrent.
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD,OEandOf are drawn to rthe sides BC,CAandAB, respecrtively. Prove that the perpendiculars from A,B,andC to the sides EF,FDandDE are concurrent.
View Solution
Knowledge Check
From a point O in the interior of a DeltaABC perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
AAF2+BD2+CE2=AE2+CD2+BF2BAB2+BC2=AC2CAF2+BD2+CE2=OA2+OB2+OC2DAF2+BD2+CE2=OD2+OE2+OF2From a point O in the interior of a ΔABC perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
AAF2+BD2+CE2=AE2+CD2+BF2BAB2+BC2=AC2CAF2+BD2+CE2=OA2+OB2+OC2DAF2+BD2+CE2=OD2+OE2+OF2In ΔABC,ADandBE are perpendiculars from A and B to the sides BC and AC, then
ACA. CE = CB. CDBCB. CA = CE. CDCADBE=ABDEDNone of these
In ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD is perpendicular to EF.
View SolutionA, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
View SolutionFrom a point P inside the triangle ABC, perpendicular PQ, PR and PS are respectively drawn to sides BC, CA and AB.
Prove that AS2+BQ2+CR2=BS2+CQ2+AR2
View SolutionProve that the perpendicular let fall from the vertices of a triangle to the opposite sides are concurrent.
View SolutionProve that the perpendicular let fall from the vertices of a triangle to the opposite sides are concurrent.
View Solution
