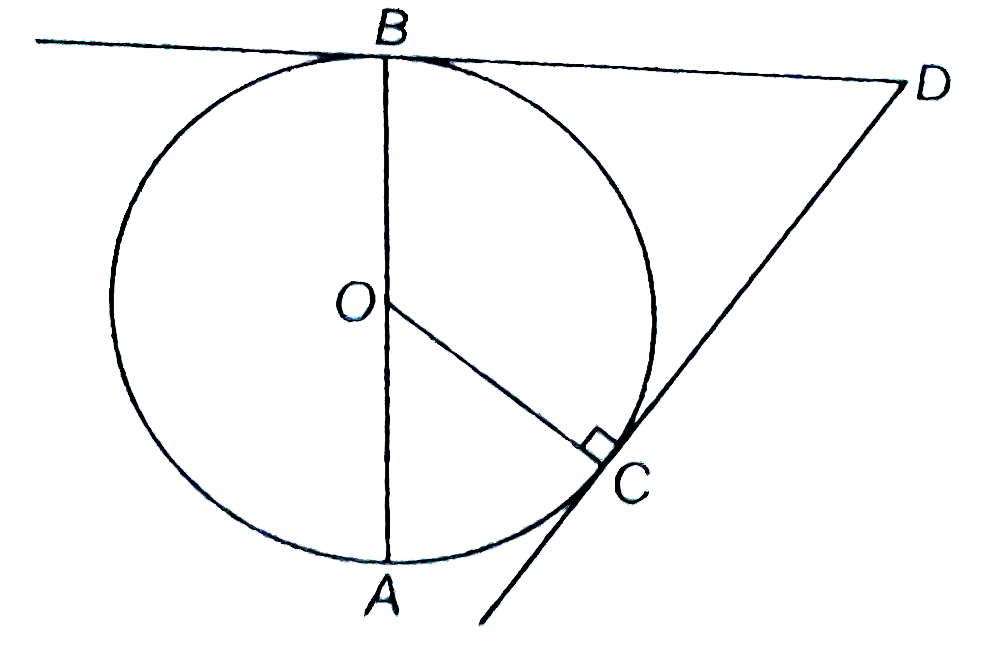
In the given figure AB is the diameter of the circle, centred at O. If ∠COA=600,AB=2r,AC=d, and CD=lSolution in Bengali
d√3
d/√3
3d
√3d/2
The correct Answer is:A

AC=d,OA=OBr,CD=BD=I,∠COA=π3
Clearly ΔAOC is equilateral
∴d=r
Also, ∠BOD=∠COD=2π3×2=π3
or tan.π3=BDOB=lr⇒l=r√3=d√3
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Multiple correct answer type24videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Linked comprehension type34videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.114videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE )8videos
PROGRESSION AND SERIES
- BOOK - CENGAGE PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - All Questions1119videos
RELATIONS AND FUNCTIONS
Similar Questions
The sides of ABC satisfy the equation 2a2+4b2+c2=4ab+2ac Then a) the triangle is isosceles b) the triangle is obtuse c) B=cos−1(78) d) A=cos−1(14)
03:37View SolutionGiven that Δ=6,r1=2,r2=3,r3=6
Circumradius R is equal to a) 2.5 b)3.5 c)1.5 d)none of these02:42View SolutionRegular pentagons are inscribed in two circles of radius 5and 2 units respectively. The ratio of their areas is
View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1|(k^2-3k+1)S_k| is ____________03:16View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1), then find f−1(x)
05:34View SolutionIn the given figure AB is the diameter of the circle, centred at O. If ∠COA=600,AB=2r,AC=d, and CD=l , then l is equal to d√3 (b) d/√3 3d (d) √3 d /2
02:01View SolutionIf AB, BC and CD are equal chords of a circle with O as centre and AD diameter, then ∠AOB= 600 (b) 900 (c) 1200 (d) none of these
04:06View SolutionIn the given figure, AB is the diameter of the circle, centered at O. If ∠COA=60∘,AB=2r,AC=d,andCD=l, then l is equal to
 02:35View Solution
02:35View SolutionIn the given figure, AB is the diameter of the circle, centered at O. If ∠COA=60∘,AB=2r,Ac=dandCD=l, then l is equal to
 02:09View Solution
02:09View SolutionIn the given figure AB is the diameter of the circle, centred at O. If ∠COA=600,AB=2r,AC=d, and CD=l , then l is equal to (a) d√3 (b) d/√3 (c) 3d (d) √3 d /2
01:45View SolutionIn the figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
01:37View SolutionIn Figure, OA and OB ar respectively perpendiculars to chords CD and EF of a circle whose centre is O. If OA=OB , prove that CE=DF.
03:05View SolutionIn Figure, O is the centre of the circle. Find ∠CBD
05:03View SolutionAB and CD are diameters of a circle with centre O. If ∠OBD=500, find ∠AOC
02:53View SolutionIf AB, BC and CD are equal chords of a circle with O as centre and AD diameter, then ∠AOB= (a) 600 (b) 900 (c) 1200 (d) none of these
05:13View SolutionAn equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOC is
03:32View Solution

