If in triangle ABC,∑sin(A2)=65and∑II1=9 (where I1,I2andI3 are excenters and I is incenter, then circumradius R is equal to 158 (b) 154 (c) 152 (d) 412Solution in Bengali
158
154
152
412
The correct Answer is:A
We know that II1=4RsinA/2
Now, ∑II1=9
⇒4R∑sin.A2=9
or 4R(65)=9 or R=158
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Multiple correct answer type24videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Linked comprehension type34videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.114videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE )8videos
PROGRESSION AND SERIES
- BOOK - CENGAGE PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - All Questions1119videos
RELATIONS AND FUNCTIONS
Similar Questions
The sides of ABC satisfy the equation 2a2+4b2+c2=4ab+2ac Then a) the triangle is isosceles b) the triangle is obtuse c) B=cos−1(78) d) A=cos−1(14)
02:06View SolutionGiven that Δ=6,r1=2,r2=3,r3=6
Circumradius R is equal to a) 2.5 b)3.5 c)1.5 d)none of these01:40View SolutionRegular pentagons are inscribed in two circles of radius 5and 2 units respectively. The ratio of their areas is
02:08View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1|(k^2-3k+1)S_k| is ____________02:19View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1), then find f−1(x)
06:54View SolutionIf A={3,6,9,12,15,18,21}, B={4,8,12,16,20},C={2,4,6,8,10,12,14,16}, D={5,10,15,20}; find
(i) A−B
(ii) A−C
(iii) A−D05:28View SolutionIf in triangle ABC,∑sinA2=65and∑II1=9 (where I1,I2andI3 are excenters and I is incenter, then circumradius R is equal to 158 (b) 154 (c) 152 (d) 412
View SolutionIf R1 is the circumradius of the pedal triangle of a given triangle ABC,andR2 is the circumradius of the pedal triangle of the pedal triangle formed, and so on R3,R4 then the value of ∞∑i=1Ri, where R (circumradius) ofABC is 5 is 8 (b) 10 (c) 12 (d) 15
01:52View SolutionThe fractional part of 24n15 is (n∈N) (A) 115 (B) 215 (C) 415 (D) none of these
02:48View SolutionCalculate the value of the electic currents I_2, I_2 and I_3 in the given electrical network. a. I_1 = ……….. b. I_2 = ………… c. I_3 = ……………
02:30View SolutionDetermine the currents I1,I2,andI3 for the network shown below
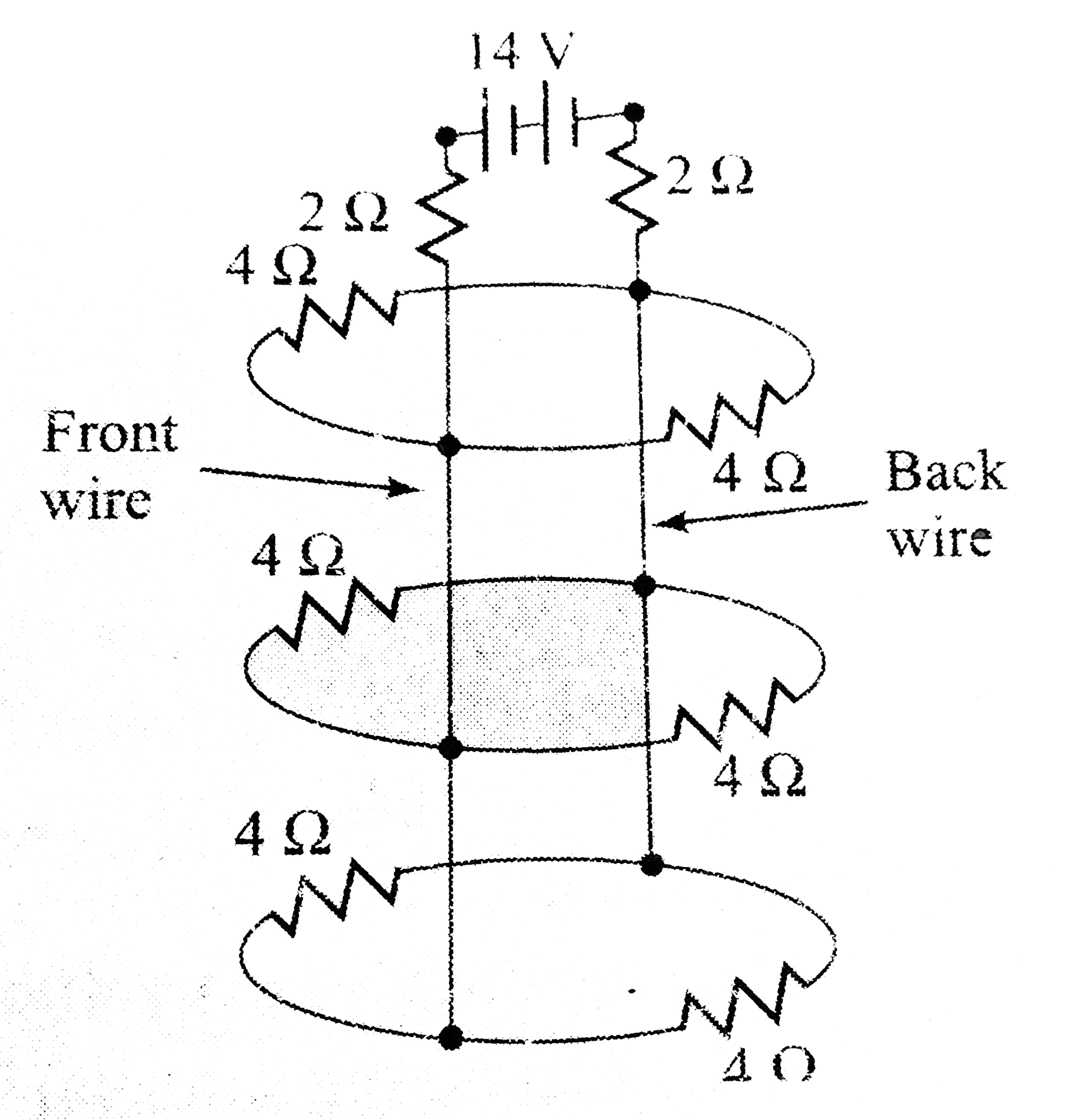
a. I1=……….,b.I2=………….,c.I3=…………….01:54View SolutionIf I is the incentre of a triangle whose is radius and circumradius are r and R respepectively : I1,I2,I3 is its ex-centre triangle, then II1.II2.II3 is equal to
04:17View SolutionIf A={3,6,9,12,15,18,21}, B={4,8,12,16,20},C={2,4,6,8,10,12,14,16}, D={5,10,15,20}; find(i) A−B (ii) A−C (iii) A−D
01:35View SolutionIf in triangle ABC,∑sin(A2)=65and∑II1=9 (where I1,I2andI3 are excenters and I is incenter, then circumradius R is equal to 158 (b) 154 (c) 152 (d) 412
08:13View SolutionThe fractional part of 24n15 is (n∈N) (A) 115 (B) 215 (C) 415 (D) none of these
04:51View SolutionIfI1=∫102x^2,I2=∫102x^3dx,I3=∫21^x2dx,I4=∫212x^3dx, then which of the following is/are ture?
a) I1>I2
(b) I2>I2
c)I3>I4
(d) I3<I402:55View Solution

