Question

Prove that, ${(1+\tan A)}^2+{(1-\tan A)}^2=2{\sec }^{2}A$

Explanation

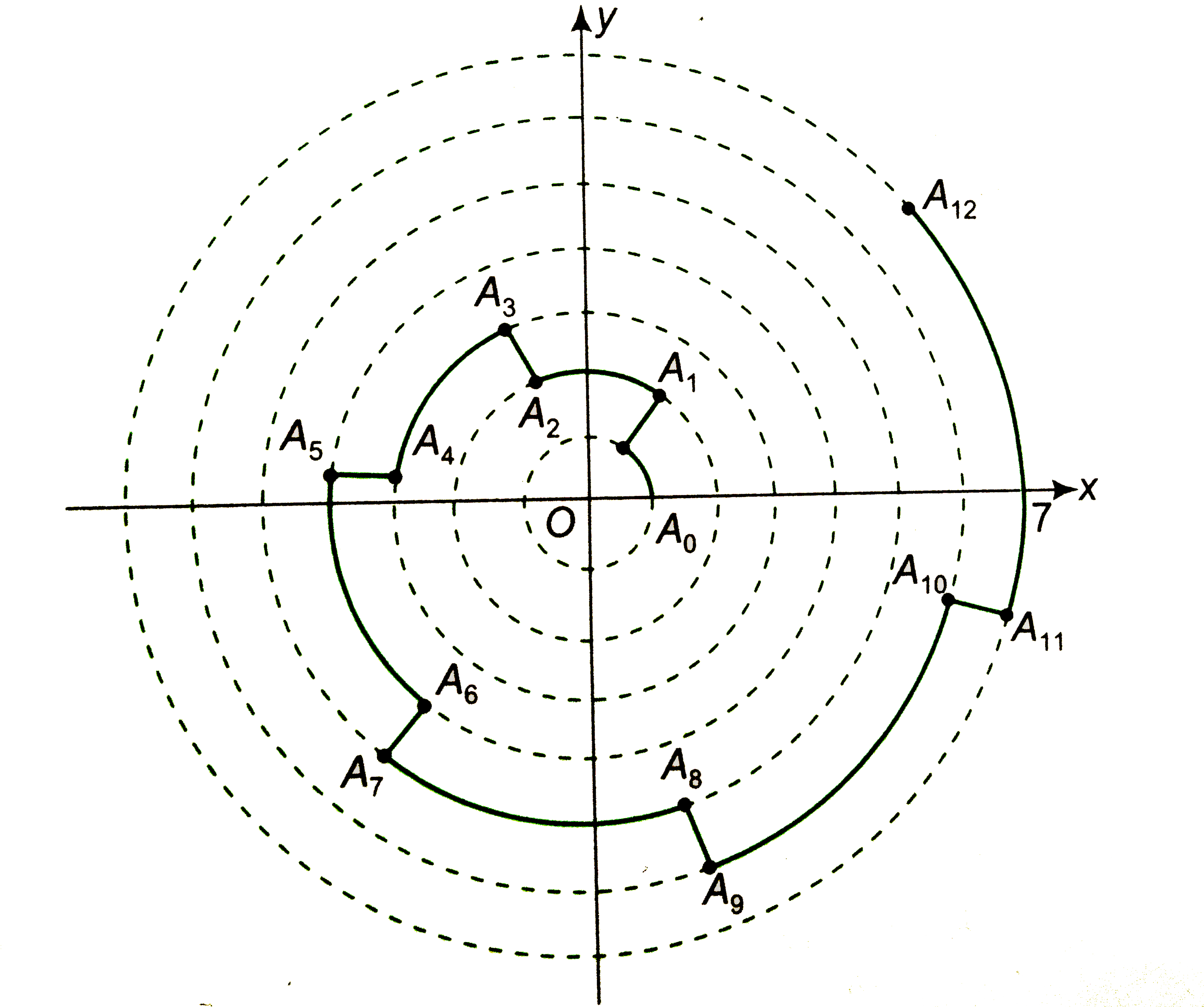
The motion of the particle on the circles is shown with bold lines in the figure starting at `A_(0)(1,0)`. Note that on every circle the particle tracels just 1 rad. The particle crosses the positive direction of the x-axis first time on `C_(n)`, where n is the least positive integer such that `nge2pirArrn=7`.