Minimum value of sec4αtan2β+sec4βtan2α, where α≠π2,β≠π2,0<α,β<π2 is_____Solution in Bengali
The correct Answer is:8
Let a=tan2α,b−tan2β
Given expression becomes
(a+1)2b+(b+1)2a(a≥,b≥0)
=a2+2a+1b+b2+2b+1a
=a2b+1b+b2a+1a+2(ab+ba)
≥4.4√a2b.1bb2a.a+2(2)
=4+4=8
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Archives JEE Main2videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Archives JEE Advanced single correct answer type1videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Matrix Match Type3videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Archives (Numerical Value Type)2videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
Similar Questions
প্রমাণ করো :tanA1−cotA+cotA1−tanA=1+tanA+cotA=1+secAcosecA
04:42View Solutionabout to only mathematics
06:16View Solution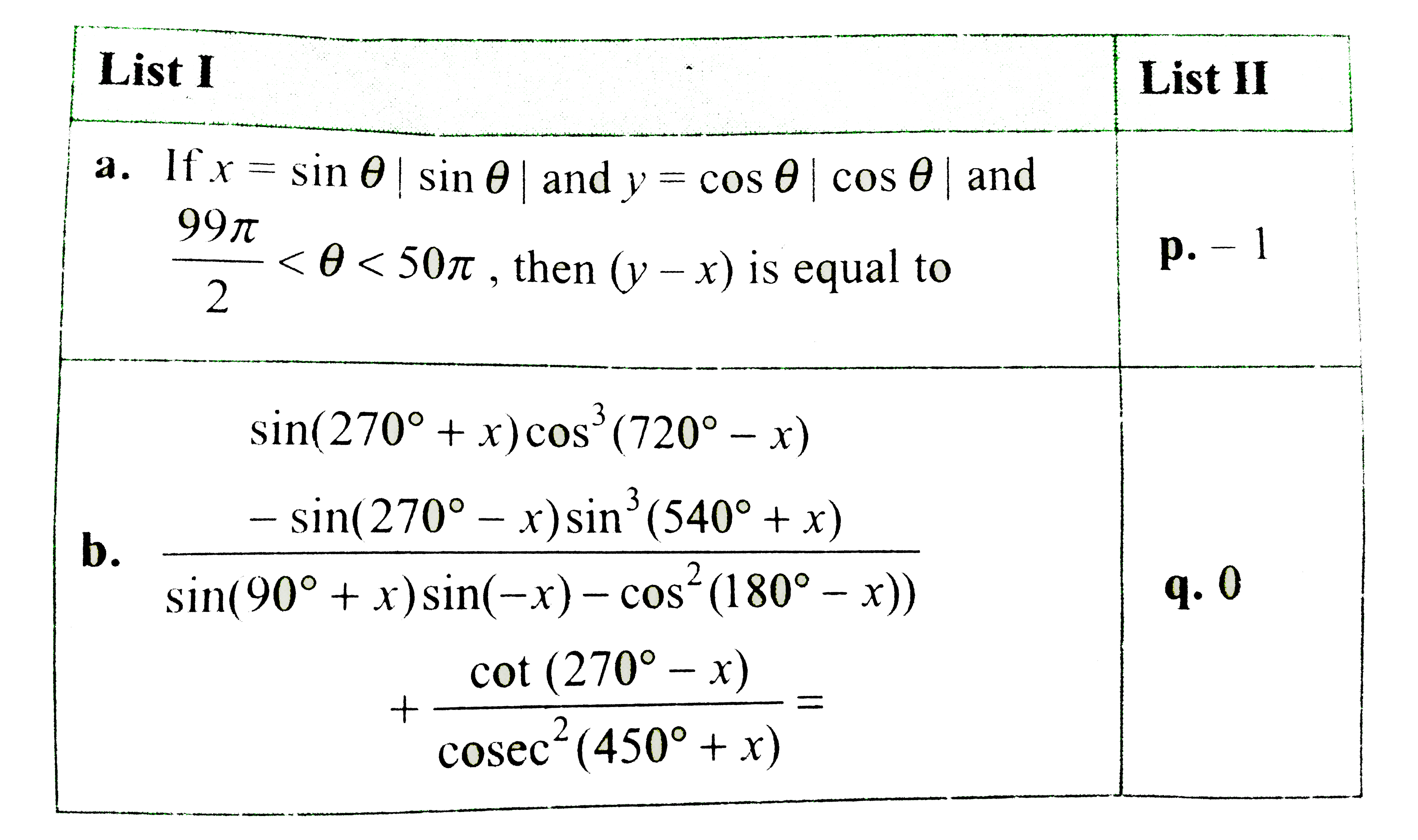
 01:49View Solution
01:49View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
04:01View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is………
04:24View SolutionMinimum value of sec4αtan2β+sec4βtan2α, where α≠π2,β≠π2,0
02:11View Solution0
05:28View SolutionIf 2sin2α=tanβ,α,β,∈(π2,π), then the value of α+β is
02:59View SolutionFind the values of tan (α+β), given that cot α=12
α∈(π,3π2)andsecβ=−53,β∈(π2,π).09:00View Solution(secα⋅secβ+tanαtanβ)2−(secα⋅tanβ+tanα⋅secβ)2 =
03:16View SolutionIf cotα=12,secβ=−53 where π<α<3π2 and π2<β<π Find the value of tan(α+β)
03:33View SolutionMinimum value of sec4αtan2β+sec4βtan2α, where α≠π2,β≠π2,0
02:55View SolutionIf 2sin2α=|tanβ+cotβ|α,β,∈(π2,π), then the value of α+β is
View SolutionIf secα is the average of sec(α−2β)andsec(α+2β) then the value of (2sin2β−sin2α) where β≠nπ is
01:31View SolutionIf sin(α+β)=1 and sin(α−β)=12, where 0≤α,β≤π2 , then find the values of tan(α+2β) and tan(2α+β) .
05:00View SolutionIf sec4αsec2β−tan4αtan2β=1 where α,β≠π2, then find the value of sec4βsec2α−tan4βtan2α
03:17View Solution

