Let x,y,z∈R+ and 2xy+3yz+4xz=18. If α, β and γ be the values of x, y and z respectively, for which xyz attains its maximum value, then the value of 2α+β+γ=
(a) 4
(b) 6
(c) 8
(d) 12Solution in Bengali
4
6
8
12
The correct Answer is:B
(b) Using A.M.≥G.M.
2xy+3yz+4xz3≥(24x2y2z2)13
⇒216≥24x2y2z2
⇒x2y2z2≤9
⇒xyz≤3
So, xyz is greatest when 2xy=3yz=4xz=6
⇒xy=3, yz=2, zx=3/2
⇒α=3/2, β=2, γ=1
2α+β+γ=6
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Comprehension2videos
INEQUALITIES INVOLVING MEANS
- BOOK - CENGAGE PUBLICATIONCHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Illustration29videos
INEQUALITIES INVOLVING MEANS
- BOOK - CENGAGE PUBLICATIONCHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer21videos
INEQUALITIES AND MODULUS
- BOOK - CENGAGE PUBLICATIONCHAPTER - INTEGRALSEXERCISE - All Questions762videos
INTEGRALS
Similar Questions
If a,b,x,y are real number and x,y>0, then a2x+b2y≥(a+b)2x+y so on solving it we have (ay−bx)2≥0.
Similarly, we can extend the inequality to three pairs of numbers, i.e,
a2x+b2y+c2z≥(a+b+c)2x+y+z
Now use this result to solve the following questions.
If abc=1 , then the minimum value of
1a3(b+c)+1b3(a+c)+1c3(a+b) is06:52View SolutionProve that (ab+xy)(ax+by)>4abxy(a,b,x,y>0).
04:33View SolutionIf f(x)=ax2+bx+c and f(−1)≥−4, f(1)≤0 and f(3)≥5, then the least value of a is
06:47View SolutionIf ∫dxx2+ax+1=f(g(x))+c, then f(x) is inverse trigonometric function for |a|>2 f(x) is logarithmic function for |a|<2 g(x) is quadratic function for |a|>2 g(x) is rational function for |a|<2
07:37View SolutionShow that the lines x−a+dα−δ=y−aα=z−a−dα+δand x−b+cβ−γ=y−bβ=z−b−cβ+γare coplanar.
View SolutionLet x,y,z∈R+ and 2xy+3yz+4xz=18. If α, β and γ be the values of x, y and z respectively, for which xyz attains its maximum value, then the value of 2α+β+γ=
07:29View Solutionदर्शाइए कि रेखाएँ
x−a+dα−δ=y−aα=z−a−dα+δ
और x−b+cβ−γ=y−bβ=z−b−cβ+γ सह-तलीय हैं |07:37View Solutionदिखाएँ कि रेखाएँ x−a+dα−δ=y−aα=z−a−dα+δ
तथा x−b+cβ−γ=y−bβ=z−b−cβ+γ समतलीय है03:04View SolutionLet P(α,β,γ)andQ(1,−1,0) be points such that the mid-point of PQ is R(x,y,z). If x is the AM of αandβ,y is the G.M. of βandγandz is the H.M . Of γandα then :
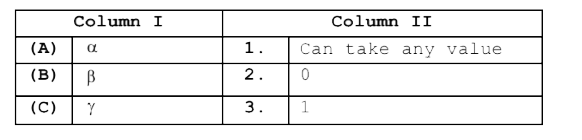 05:03View Solution
05:03View Solutionदर्शाइए की रेखाएँ
x−a+dα−δ=y−aα=z−a−dα+δ और x−b+cβ−γ=y−bβ=z−b−cβ+γ सह-तलीय है |05:05View Solutionदर्शाइए की रेखाएं
x−a+dα−δ=y−aα=z−a−dα+δ और x−b+cβ−γ=y−bβ=z−b−cβ+γ समतलीय है04:00View SolutionIf α,β,γ are the cube roots of a negative number p, then for any three real numbers x,y,z the value of xα+yβ+zγxβ+yγ+zα is
10:25View SolutionShow that the lines x−a+dα+δ=y−aα=z−a−dα+δ and x−b+cβ+γ=y−bβ=z−b−cβ+γ are coplanar.
06:34View SolutionShow that the lines x−a+dα−δ=y−aα=z−a−dα+δ and x−b+cβ−γ=y−bβ=z−b−cβ+γ are coplanar.
03:18View SolutionLet x,y,z∈R+ and 2xy+3yz+4xz=18. If α, β and γ be the values of x, y and z respectively, for which xyz attains its maximum value, then the value of 2α+β+γ=
07:34View SolutionShow that the lines x−a+dα−δ=y−aα=z−a−dα+δ and x−b+cβ−γ=y−bβ=z−b−cβ+γ are coplanar.
04:46View Solution

