Let f:R→R be a continuous onto function satisfying f(x)+f(−x)=0∀x∈R. If f(−3)=2 and f(5)=4 in [−5,5], then the minimum number of roots of the equation f(x)=0 isSolution in Bengali
The correct Answer is:3
f(x)+f(−x)=0
Therefore,f(x) is an odd function.
Since points (-3, 2) and (5, 4) lie on the curve,
∴ (3, -2) and (-5, -4) will also lie on the curve.
For minimum number of roots, graph of continuous function f(x) is as follows:
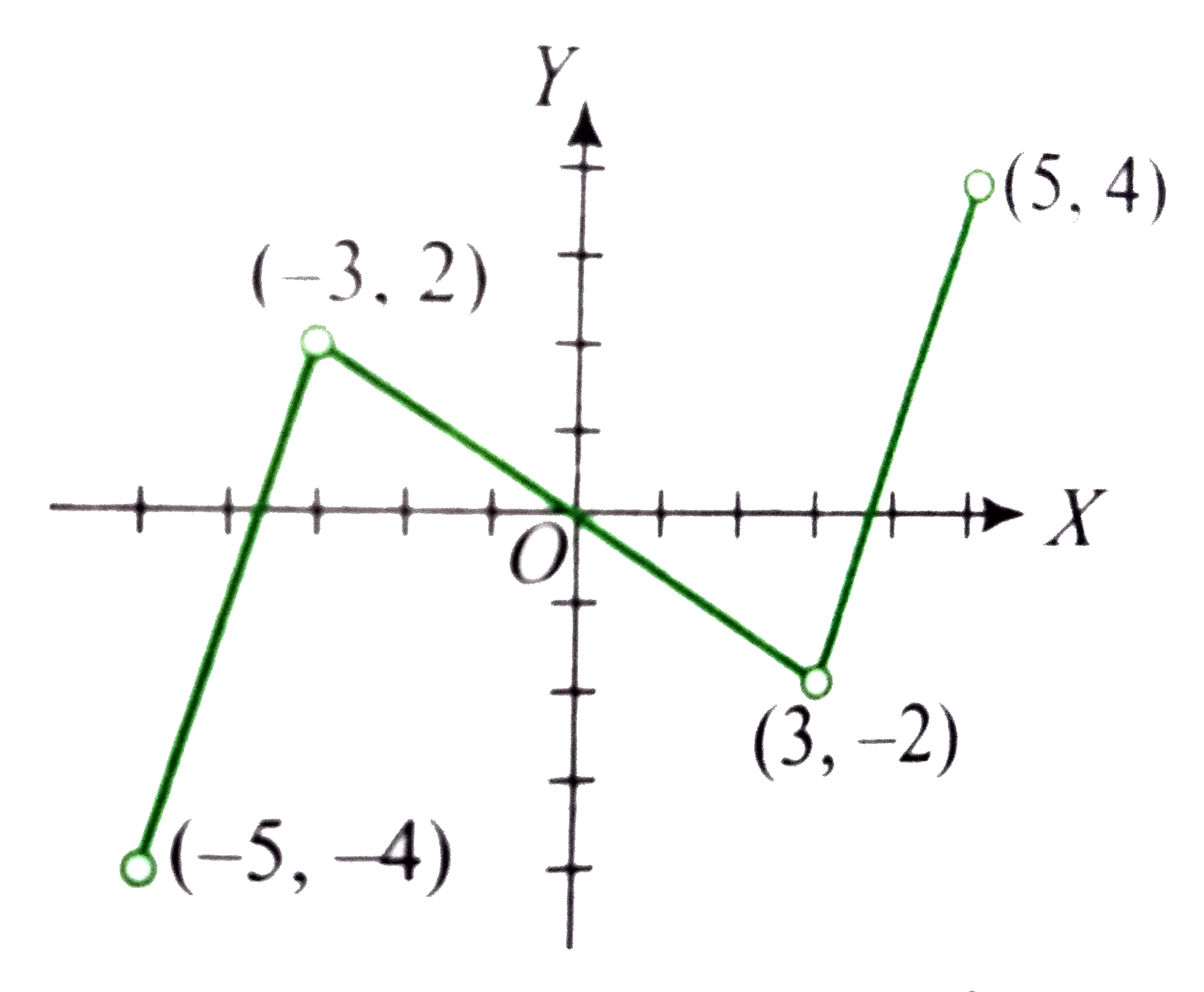
From the above graph of f(x), it is clear that equation f(x)=0 has at least three real roots.
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
04:42View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 602:36View SolutionLet f:R→R be a continuous onto function satisfying f(x)+f(−x)=0∀x∈R. If f(−3)=2andf(5)=4∈[−5,5], then the minimum number of roots of the equation f(x)=0 is
05:12View SolutionLet f be a function satisfying f(x+y)=f(x) *f(y) for all x,y, in R. If f (1) =3 then sum_(r=1)^(n) f (r) is equal to
View SolutionLet f:R rarr R be a continuous onto function satisfying f(x)+f(-x)=0AA x in R, If f(-3)=2 and f(5)=4 in [-5,5], then the equation f(x)=0 has
View SolutionLet f:R→R be a continuous onto function satisfying f(x)+f(−x)=0,∀x∈R . If f(−3)=2andf(5)=4 in [-5, 5], then what is the minimum number of roots of the equation f(x) = 0?
02:15View SolutionLet a function f:R→R, where R is the set of real nos. satisfying the equation f(x+y)=f(x)+f(y)∀x,y if f(x) is continuous at x = 0, then
View SolutionLet f(x) be a continuous & differentiable function on R satisfying f(−x)=f(x)&f(3+x)=f(3−x)∀x∈R. If f'(1)=−5 then f'(7) =
06:23View SolutionLet f be a continuous function satisfying f(x) f(y)=f(x)+f(y)+f(xy)-2 for all x,y ∈ R and f(2)=5 then limx→4f(x) is
04:52View SolutionLet f:R→R be a continuous onto function satisfying f(x)+f(−x)=0∀x∈R. If f(−3)=2 and f(5)=4 in [−5,5], then the minimum number of roots of the equation f(x)=0 is
05:12View SolutionLet f:R→R be a continuous onto function satisfying f(x)+f(−x)=0,∀x∈R . If f(−3)=2andf(5)=4 in [-5, 5], then what is the minimum number of roots of the equation f(x) = 0?
02:12View SolutionLet a function f: R to R , where R is the set of real nos. satisfying the equation f(x+y) = f(x) + f(y) AA x, y if f(x) is continuous at x = 0, then
04:14View Solutionएक सतत् एवं आच्छादक फलन f:R→R इस प्रकार से है कि f(x)+f(−x)=0,∀x∈R. यदि f(-3)=2 तथा f(5)=4 तो अन्तराल [-5,5], में f(x)=0 का-
03:08View SolutionLet f:R→R be a function satisfying f(2−x)=f(2+x)andf(20−x)=f(x)∀x∈R.For this functions f. answer the following
The graph of y = f(x) is not symmetrical about02:32View SolutionLet f: R→R be a function defined as f (x) = 3x+ 7 , x∈R . Show that f is an onto functions.
04:42View SolutionLet f : R→ R be a continuous function which satisfies f(x)=∫x0f(t)dt. Then the value of f(loge5) is
03:32View Solution
