A curve is given by byy={(√4−x2),0≤x<1√(3x),1≤x≤3. Find the area lying between the curve and x-axis.Solution in Bengali
The correct Answer is:16(2π−√3+36) sq. units
The given curve is
y={√(4−x2),0≤x<1√(3x),1≤x≤3
Obviously, the curve is the are of the circle x2+y2=4 (1)
between 0≤x<1 and the are of parabola y2=3x (2)
between 1≤x≤3
Required area = shaded area
=Area OABCO+Area CBDEC
=∣∣∣∫10√(4−x2)dx∣∣∣+∣∣∣∫31√3xdx∣∣∣
∣∣∣[12x√(4−x2)+42sin−1(x2)]10∣∣∣+∣∣∣√3[23x3/2]31∣∣∣
=(√32+π3)+23(9−√3)
=16(2π−√3+36) sq. units.
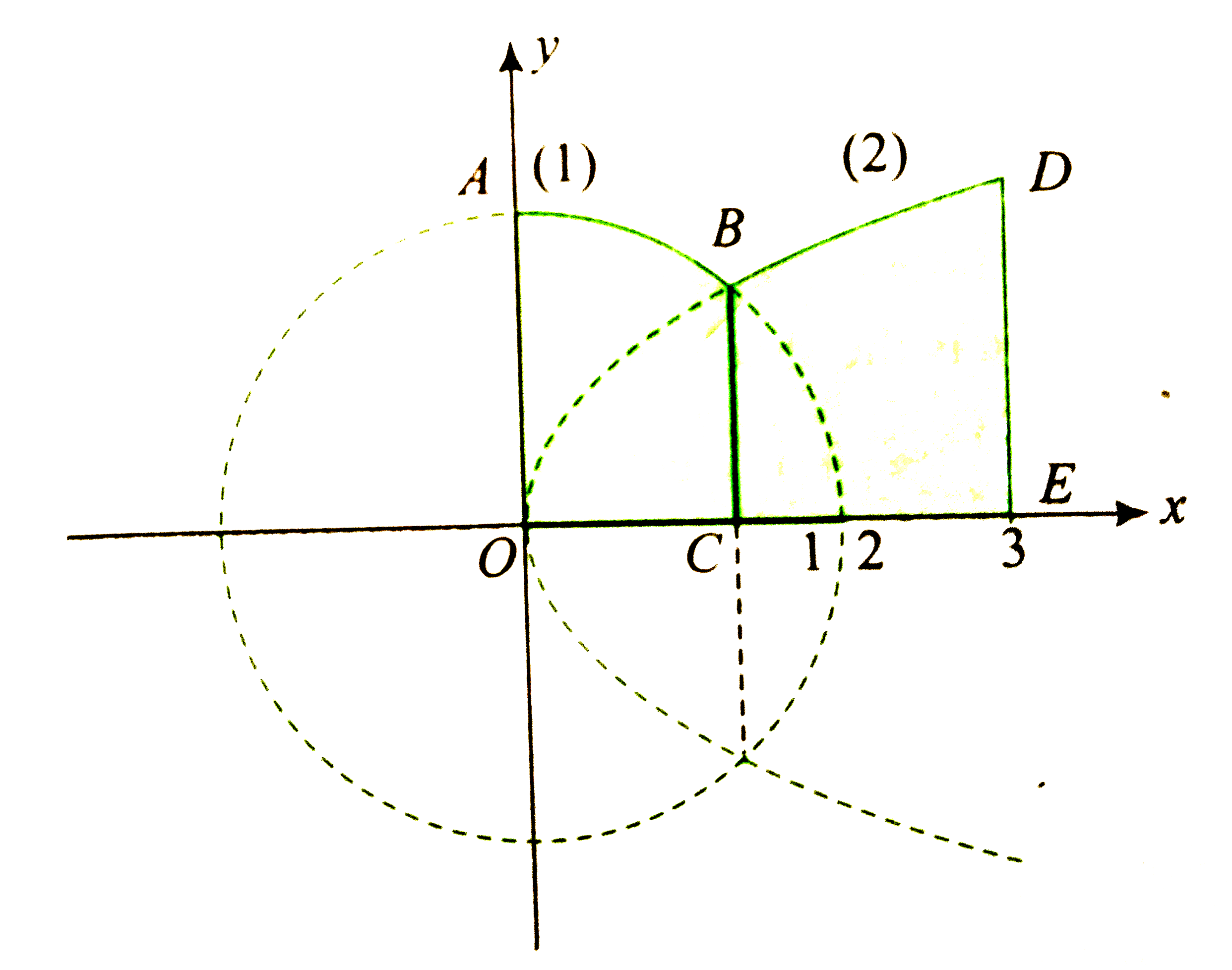
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.214videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.37videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Solved Examples10videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
Similar Questions
Find the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
09:58View SolutionFind the continuous function f where (x4−4x2)≤f(x)≤(2x2−x3) such that the area bounded by y=f(x),y=x4−4x2. then y-axis, and the line x=t, where (0≤t≤2) is k times the area bounded by y=f(x),y=2x2−x3,y-axis , and line x=t(where0≤t≤2).
08:37View SolutionFind the area bounded by the curve x2=y,x2=−yandy2=4x−3
03:54View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
02:37View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is05:19View SolutionA curve is given by y={(√4−x2),0≤x<1and√(3x),1≤x≤3. Find the area lying between the curve and x-axis.
03:27View SolutionThe area bounded by the curve y=(x-1)(x-2)(x-3) and x -axis lying between the ordinates x=0 and x=4 is
11:51View SolutionThe area of the region lying between the line x-y+2=0 and the curve x=sqrt(y)and y-axis , is
08:43View SolutionIf A is the area lying between the curve y=sin x and x-axis between x=0 and x=pi//2 . Area of the region between the curve y=sin 2x and x -axis in the same interval is given by
04:05View SolutionLet the curve y=ax12 +bx passes through the point (1,2) and lies above the axis for 0<x<9 .If the area enclosed by the curve the x-axis and the line x =4 is 8 eq. units Then-
05:30View Solutionसमाकलन की सहायता से वक्र y=√3x+4 का x-अक्ष तथा सीमाओं x=0 और x=4 के मध्य स्थित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
11:19View Solutionवक्र y=√4−x2,x=√3y तथा x- अक्ष के मध्य घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
02:21View SolutionA curve is given by y={(√4−x2),0≤x<1and√(3x),1≤x≤3. Find the area lying between the curve and x-axis.
05:45View SolutionA curve is given by byy={(√4−x2),0≤x<1√(3x),1≤x≤3. Find the area lying between the curve and x-axis.
03:37View SolutionIf the curve y = sqrt(3x+4) The area of the area bounded between the line x = - 1 and x = 4 and x - axis is A and the curve y^(2)=3x+4 , Is the area of the area bounded between the line x = - 1 and x = 4 and the axis, then the value of A: B is
07:40View SolutionThe area bounded by the curve y=(x−1)(x−2)(x−3) and x-axis lying between the ordinates x=0andx=4 is
05:38View Solution

