Find tha area of the region containing the points satisfying . Solution in Bengali
8 sq. units
2 sq. units
sq. units
sq. units
The correct Answer is:A
The points in the required region satisfy
Since the curve (1) is symmetrical about both the axes, the required area is 4 times the area of the region in the first quadrant. Therefore, it is sufficient to sketch the region and to find the area in the first quadrant.
In the first quadrant, the curve (1) consist of two curves
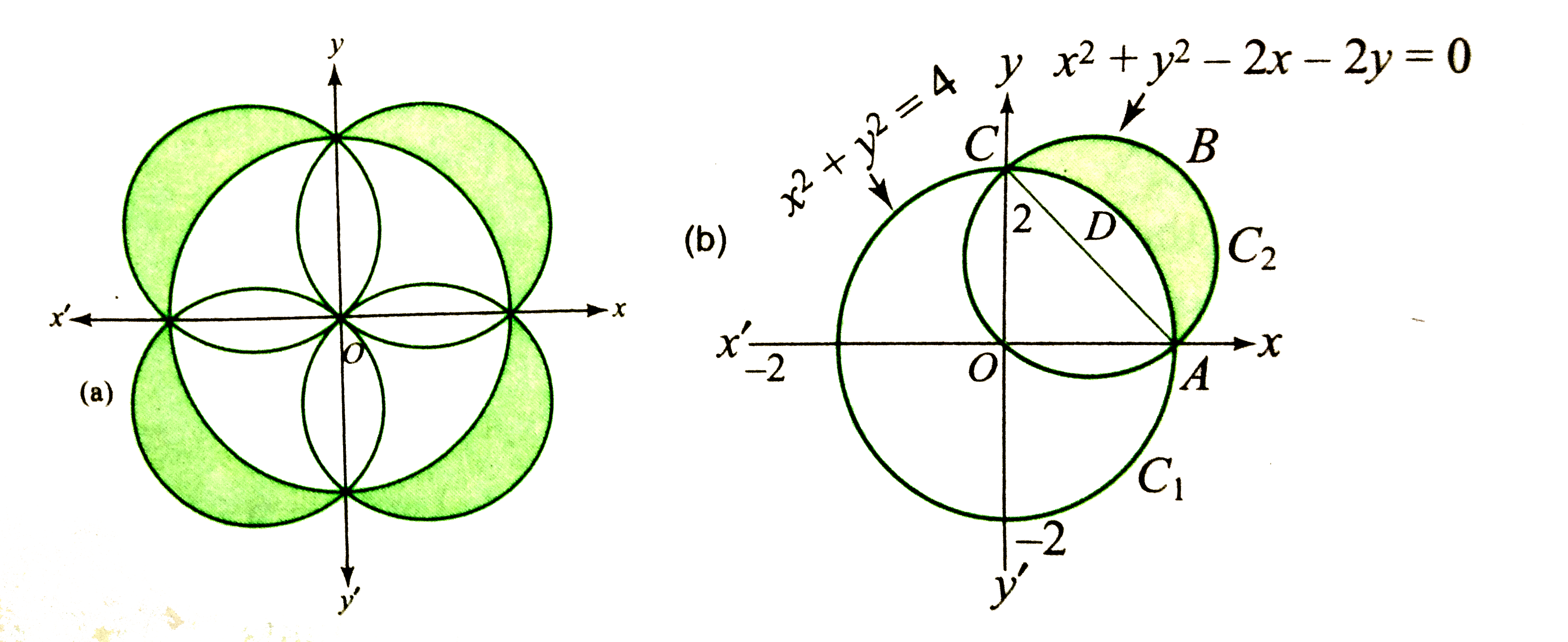
Required area =4 (area ABCDA)
=4(area of semi-cirlce ABCA)-(area of sector ADCBA)
=4(area of semi-circle ABCA)-(area of sector OADCO-area of triangle OAC)
sq. units.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Multiple Correct Answers Type13videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Linkded Comprehension Type21videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.37videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
Similar Questions
Let A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
View SolutionLet Ar be the area of the region bounded between the curves y2=(e−kr)x(where k>0,r∈N) and the line y=mx(where m≠0), k and m are some constants
A1,A2,A3,… are in G.P. with common ratio11:50View SolutionFind the continuous function f where (x4−4x2)≤f(x)≤(2x2−x3) such that the area bounded by y=f(x),y=x4−4x2. then y-axis, and the line x=t, where (0≤t≤2) is k times the area bounded by y=f(x),y=2x2−x3,y-axis , and line x=t(where0≤t≤2).
05:54View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
03:05View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is03:09View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
04:24View SolutionFind the area of the region formed by the points satisfying
|x|+|y|+|x+y|≤2.10:00View SolutionThe area (in sq units) of the region
A={(x,y):y22≤x≤y+4} is11:42View SolutionFind the area of the region [x,y):x2+y2≤1≤x+y}
13:01View SolutionFind the area of the region {(x,y):x2+y2≤2ax , y2≤ax , x≤0 , y≤0}
08:00View SolutionThe area of the region bounded by the curves {(x,y):x2+y2≤4,2≤x+y} is __________ .
07:31View Solutionक्षेत्र {(x,y):0≤y≤x2+1,y≤x+1,0≤x≤2} का क्षेत्रफल ज्ञात कीजिए।
03:44View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
05:17View SolutionFind the area of the region formed by the points satisfying
|x|+|y|+|x+y|≤2.08:36View SolutionFind the area bounded by the region given by : A={(x,y):x29+y24≤1≤x3+y2}.
04:01View Solution

